
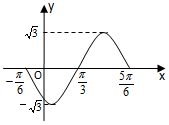
 函数f(x)=Asin(ωx+ϕ)(A>0,ω>0,|ϕ|<π)在一个周期上的图象如图所示,
函数f(x)=Asin(ωx+ϕ)(A>0,ω>0,|ϕ|<π)在一个周期上的图象如图所示,分析 (1)由函数的图象的顶点坐标求出A,由周期求出ω,由五点法作图求出φ的值,从而求得函数的解析式.
(2)利用正弦函数的单调性,求得函数f(x)的单调递减区间.
(3)由条件求得cosα的值,再利用同角三角函数的基本关系求得sinα的值.
解答 解:(1)根据函数f(x)=Asin(ωx+ϕ)(A>0,ω>0,|ϕ|<π)在一个周期上的图象,
可得A=$\sqrt{3}$,$\frac{2π}{ω}$=$\frac{5π}{6}$+$\frac{π}{6}$,∴ω=2,
再根据五点法作图可得2•$\frac{π}{3}$+φ=0,∴ω=-$\frac{2π}{3}$,∴$f(x)=\sqrt{3}sin(2x-\frac{2π}{3})$.
(2)令2kπ+$\frac{π}{2}$≤2x-$\frac{2π}{3}$≤2kπ+$\frac{3π}{2}$,求得kπ+$\frac{7π}{12}$≤x≤kπ+$\frac{13π}{12}$,可得函数的减区间为$[{\frac{7π}{12}+kπ,\frac{13π}{12}+kπ}]k∈Z$.
(3)若$f(\frac{α}{2}+\frac{7π}{12})=\frac{{3\sqrt{3}}}{5},α∈[-\frac{5π}{2},-2π]$,则$\sqrt{3}$sin(α+$\frac{7π}{6}$-$\frac{2π}{3}$)=$\sqrt{3}$sin(α+$\frac{π}{2}$)=$\sqrt{3}$cosα=$\frac{3\sqrt{3}}{5}$,
∴cosα=$\frac{3}{5}$,∴sinα=-$\sqrt{{1-cos}^{2}α}$=-$\frac{4}{5}$.
点评 本题主要考查由函数y=Asin(ωx+φ)的部分图象求解析式,由函数的图象的顶点坐标求出A,由周期求出ω,由五点法作图求出φ的值.还考查了正弦函数的单调性,同角三角函数的基本关系,属于基础题.


 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{asinαsinβ}{sin(β-α)}$ | B. | $\frac{asinαcosβ}{sin(β-α)}$ | C. | $\frac{acosαsinβ}{sin(β-α)}$ | D. | $\frac{asinαsinβ}{cos(β-α)}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图所示,PA⊥平面ABCD,底面ABCD为菱形,$∠ABC=\frac{π}{3}$,PA=AB=4,AC交BD于O,点N是PC的中点.
如图所示,PA⊥平面ABCD,底面ABCD为菱形,$∠ABC=\frac{π}{3}$,PA=AB=4,AC交BD于O,点N是PC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①② | B. | ①②③ | C. | ②④ | D. | ①③ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | b<a<c | B. | c<b<a | C. | a<b<c | D. | b<c<a |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| t/时 | 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
| y/米 | 2 | $\frac{3}{2}$ | 1 | $\frac{3}{2}$ | 2 | $\frac{3}{2}$ | 0.99 | $\frac{3}{2}$ | 2 |
| A. | y=$\frac{1}{2}$cos$\frac{π}{6}$t+1 | B. | y=$\frac{1}{2}$cos$\frac{π}{6}$t+$\frac{3}{2}$ | C. | y=2cos$\frac{π}{6}$t+$\frac{3}{2}$ | D. | y=$\frac{1}{2}$cos6πt+$\frac{3}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-1,+∞) | B. | (-1,+∞) | C. | [-2,+∞) | D. | (-2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com