
【题目】某项考试按科目A、科目B依次进行,只有当科目A成绩合格时,才可继续参加科目B的考试.已知每个科目只允许有一次补考机会,两个科目成绩均合格方可获得证书.现某人参加这项考试,科目A每次考试成绩合格的概率均为![]() ,科目B每次考试成绩合格的概率均为
,科目B每次考试成绩合格的概率均为![]() .假设各次考试成绩合格与否均互不影响.
.假设各次考试成绩合格与否均互不影响.
(1)求他不需要补考就可获得证书的概率;
(2)在这项考试过程中,假设他不放弃所有的考试机会,记他参加考试的次数为![]() ,求
,求![]() 的分布列及数学期望E
的分布列及数学期望E![]() .
.
【答案】(1)![]()
(2)
| 2 | 3 | 4 |
P |
|
|
|
![]()
【解析】![]()
试题分析:(1)不需要补考就获得证书的事件表示科目![]() 第一次考试合格且科目
第一次考试合格且科目![]() 第一次考试合格,这两次考试合格是相互独立的,根据相互独立事件同时发生的概率,得到结果.
第一次考试合格,这两次考试合格是相互独立的,根据相互独立事件同时发生的概率,得到结果.
(2)参加考试的次数为![]() ,由已知得,
,由已知得,![]() 注意到各事件之间的独立性与互斥性,根据相互独立事件同时发生的概率写出概率,得到
注意到各事件之间的独立性与互斥性,根据相互独立事件同时发生的概率写出概率,得到![]() 的分布列并求出期望
的分布列并求出期望![]() .
.
试题解析:解:设“科目A第一次考试合格”为事件A1,“科目A补考合格”为事件A2;“科目B第一次考试合格”为事件B1,“科目B补考合格”为事件B2..............1分
(1)不需要补考就获得证书的事件为A1·B1,注意到A1与B1相互独立,
则![]() .
.
该考生不需要补考就获得证书的概率为![]() ..............4分
..............4分
(2)由已知得,![]() =2,3,4,注意到各事件之间的独立性与互斥性,可得
=2,3,4,注意到各事件之间的独立性与互斥性,可得
![]()
![]() .............6分
.............6分
![]()
![]() 8分
8分
![]() 10分
10分
| 2 | 3 | 4 |
P |
|
|
|
故![]()
答:该考生参加考试次数的数学期望为![]() 12分
12分


 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(Ⅰ)若f(1)=0,求函数f(x)的最大值;
(Ⅱ)令![]() ,讨论函数g(x)的单调区间;
,讨论函数g(x)的单调区间;
(Ⅲ)若a=2,正实数x1,x2满足![]() 证明
证明![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知直四棱柱ABCD-A1B1C1D1的底面是菱形,且∠DAB=60°,AD=AA1,F为棱BB1的中点,M为线段AC1的中点.

(1)求证:直线MF∥平面ABCD;
(2)求证:平面AFC1⊥平面ACC1A1.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,且过点
,且过点![]() .
.
(Ⅰ)求椭圆![]() 的方程.
的方程.
(Ⅱ)若![]() ,
, ![]() 是椭圆
是椭圆![]() 上两个不同的动点,且使
上两个不同的动点,且使![]() 的角平分线垂直于
的角平分线垂直于![]() 轴,试判断直线
轴,试判断直线![]() 的斜率是否为定值?若是,求出该值;若不是,说明理由.
的斜率是否为定值?若是,求出该值;若不是,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】全世界越来越关注环境保护问题,某省一监测站点于2016年8月某日起连续![]() 天监测空气质量指数
天监测空气质量指数![]() ,数据统计如下:
,数据统计如下:

(Ⅰ)根据所给统计表和频率分布直方图中的信息求出![]() 、
、![]() 的值,并完成频率分布直方图;
的值,并完成频率分布直方图;
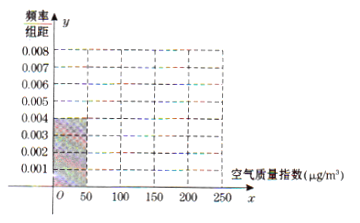
(Ⅱ)在空气质量指数分别为![]() 和
和![]() 的监测数据中,用分层抽样的方法抽取5天,从中任意选取2天,求事件
的监测数据中,用分层抽样的方法抽取5天,从中任意选取2天,求事件![]() “两天空气都为良”发生的概率.
“两天空气都为良”发生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C的对边分别是a,b,c已知ccosB+(b-2a)cosC=0
(1)求角C的大小
(2)若c=2,a+b=ab,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() ,其中
,其中![]() 为自然对数的底数.
为自然对数的底数.
(Ⅰ)若曲线![]() 在
在![]() 轴上的截距为-1,且在点
轴上的截距为-1,且在点![]() 处的切线垂直于直线
处的切线垂直于直线![]() ,求实数
,求实数![]() 的值;
的值;
(Ⅱ)记![]() 的导函数为
的导函数为![]() ,
, ![]() 在区间
在区间![]() 上的最小值为
上的最小值为![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在党的群众教育路线总结阶段,一督导组从某单位随机抽调25名员工,让他们对单位的各项开展工作进行打分评价,现获得如下数据:70,82,81,76,84,80,77,77,65,85,69,83,71,76,89,74,73,83,78,82,72,74,86,79,76.
(1)根据上述数据完成样本的频率分布表;
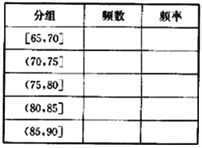
(2)根据(1)的频率分布表,完成样本分布直方图;

(3)从区间![]() 和
和![]() 中任意抽取两个评分,求两个评分来自不同区间的概率.
中任意抽取两个评分,求两个评分来自不同区间的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)由数字1、2、3、4、5、6、7组成无重复数字的七位数
求三个偶数必相邻的七位数的个数及三个偶数互不相邻的七位数的个数
(2)六本不同的书,分为三组,求在下列条件下各有多少种不同的分配方法?
(I)每组两本
(II)一组一本,一组二本,一组三本.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com