
【题目】阅读右面的程序框图,运行相应的程序,若输入N的值为24,则输出N的值为( )
A.0
B.1
C.2
D.3
【答案】C
【解析】解:第一次N=24,能被3整除,N= ![]() ≤3不成立,
≤3不成立,
第二次N=8,8不能被3整除,N=8﹣1=7,N=7≤3不成立,
第三次N=7,不能被3整除,N=7﹣1=6,N= ![]() =2≤3成立,
=2≤3成立,
输出N=2,
故选:C
【考点精析】利用算法的条件结构和算法的循环结构对题目进行判断即可得到答案,需要熟知条件P是否成立而选择执行A框或B框.无论P条件是否成立,只能执行A框或B框之一,不可能同时执行A框和B框,也不可能A框、B框都不执行.一个判断结构可以有多个判断框;在一些算法中,经常会出现从某处开始,按照一定条件,反复执行某一处理步骤的情况,这就是循环结构,循环结构可细分为两类:当型循环结构和直到型循环结构.


科目:高中数学 来源: 题型:
【题目】在亚丁湾海域执行护航任务的中国海军“徐州”舰,在A处收到某商船在航行中发出求救信号后,立即测出该商船在方位角方位角(是从某点的指北方向线起,依顺时针方向到目标方向线之间的水平夹角)为45°、距离A处为10 n mile的C处,并测得该船正沿方位角为105°的方向,以9 n mile/h的速度航行,“徐州”舰立即以21 n mile/h的速度航行前去营救.
(1)“徐州”舰最少需要多少时间才能靠近商船?
(2)在营救时间最少的前提下,“徐州”舰应按照怎样的航行方向前进?(角度精确到0.1°,时间精确到1min,参考数据:sin68.2°≈0.9286)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是菱形,
是菱形,![]() ,
,![]() 为等边三角形,
为等边三角形,![]() 是线段
是线段![]() 上的一点,且
上的一点,且![]() 平面
平面![]() .
.

(1)求证:![]() 为
为![]() 的中点;
的中点;
(2)若![]() 为
为![]() 的中点,连接
的中点,连接![]() ,
,![]() ,
,![]() ,
,![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() ,求三棱锥
,求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“开门大吉”是中央电视台推出的娱乐节目.选手面对1~8号8扇大门,依次按响门上的门铃,门铃会播放一段音乐的单音色旋律,选手需正确回答出这首歌的名字,方可获得该扇门对应的家庭梦想基金.在一次场外调查中,发现参赛选手多数分为两个年龄段:20~30;30~40(单位:岁),其猜对歌曲名称与否的人数如图所示.

(Ⅰ) 完成下列2×2列联表;
正误 年龄 | 正确 | 错误 | 合计 |
20~30 | 30 | ||
30~40 | 70 | ||
合计 | 120 |
(Ⅱ)判断是否有90%的把握认为猜对歌曲名称与否和年龄有关;说明你的理由.(下面的临界值表供参考)
| 0.10 | 0.05 | 0.010 | 0.005 |
| 2.706 | 3.841 | 6.635 | 7.879 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在△ABC中,AB的中点为O,且OA=1,点D在AB的延长线上,且 ![]() .固定边AB,在平面内移动顶点C,使得圆M与边BC,边AC的延长线相切,并始终与AB的延长线相切于点D,记顶点C的轨迹为曲线Γ.以AB所在直线为x轴,O为坐标原点如图所示建立平面直角坐标系.
.固定边AB,在平面内移动顶点C,使得圆M与边BC,边AC的延长线相切,并始终与AB的延长线相切于点D,记顶点C的轨迹为曲线Γ.以AB所在直线为x轴,O为坐标原点如图所示建立平面直角坐标系. 
(Ⅰ)求曲线Γ的方程;
(Ⅱ)设动直线l交曲线Γ于E、F两点,且以EF为直径的圆经过点O,求△OEF面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】执行两次如图所示的程序框图,若第一次输入的x值为7,第二次输入的x值为9,则第一次,第二次输出的a值分别为( )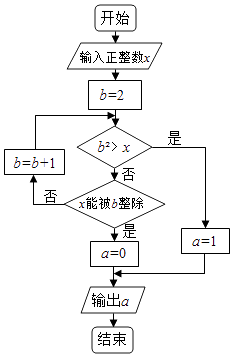
A.0,0
B.1,1
C.0,1
D.1,0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f (x)=ex+2x2-3x.
(1)求证:函数f (x)在区间[0,1]上存在唯一的极值点.
(2)当x≥![]() 时,若关于x的不等式f (x)≥
时,若关于x的不等式f (x)≥![]() x2+(a-3)x+1恒成立,试求实数a的取值范围.
x2+(a-3)x+1恒成立,试求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合![]() 是满足下列条件的函数
是满足下列条件的函数![]() 的全体:在定义域内存在实数
的全体:在定义域内存在实数![]() ,使得
,使得![]() 成立.
成立.
(Ⅰ)判断幂函数![]() 是否属于集合
是否属于集合![]() ?并说明理由;
?并说明理由;
(Ⅱ)设![]() ,
, ![]() ,
,
i)当![]() 时,若
时,若![]() ,求
,求![]() 的取值范围;
的取值范围;
ii)若对任意的![]() ,都有
,都有![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】元旦期间,某轿车销售商为了促销,给出了两种优惠方案,顾客只能选择其中的一种,方案一:每满![]() 万元,可减
万元,可减![]() 千元;方案二:金额超过
千元;方案二:金额超过![]() 万元(含
万元(含![]() 万元),可摇号三次,其规则是依次装有
万元),可摇号三次,其规则是依次装有![]() 个幸运号、
个幸运号、![]() 个吉祥号的一个摇号机,装有
个吉祥号的一个摇号机,装有![]() 个幸运号、
个幸运号、![]() 个吉祥号的二号摇号机,装有
个吉祥号的二号摇号机,装有![]() 个幸运号、
个幸运号、![]() 个吉祥号的三号摇号机各摇号一次,其优惠情况为:若摇出
个吉祥号的三号摇号机各摇号一次,其优惠情况为:若摇出![]() 个幸运号则打
个幸运号则打![]() 折,若摇出
折,若摇出![]() 个幸运号则打
个幸运号则打![]() 折;若摇出
折;若摇出![]() 个幸运号则打
个幸运号则打![]() 折;若没有摇出幸运号则不打折.
折;若没有摇出幸运号则不打折.
(1)若某型号的车正好![]() 万元,两个顾客都选中第二中方案,求至少有一名顾客比选择方案一更优惠的概率;
万元,两个顾客都选中第二中方案,求至少有一名顾客比选择方案一更优惠的概率;
(2)若你评优看中一款价格为![]() 万的便型轿车,请用所学知识帮助你朋友分析一下应选择哪种付款方案.
万的便型轿车,请用所学知识帮助你朋友分析一下应选择哪种付款方案.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com