
【题目】某制造厂商10月份生产了一批乒乓球,从中随机抽取![]() 个进行检查,测得每个球的直径(单位:
个进行检查,测得每个球的直径(单位:![]() ),将数据进行分组,得到如下频率分布表:
),将数据进行分组,得到如下频率分布表:

(1)求![]() 、
、![]() 、
、![]() 及
及![]() 、
、![]() 的值,并画出频率分布直方图(结果保留两位小数);
的值,并画出频率分布直方图(结果保留两位小数);
(2)已知标准乒乓球的直径为![]() ,直径误差不超过
,直径误差不超过![]() 的为五星乒乓球,若这批乒乓球共有
的为五星乒乓球,若这批乒乓球共有![]() 个,试估计其中五星乒乓球的数目;
个,试估计其中五星乒乓球的数目;
(3)统计方法中,同一组数据常用该组区间的中点值(例如区间![]() 的中点值是
的中点值是![]() )作为代表,估计这批乒乓球直径的平均值和中位数.
)作为代表,估计这批乒乓球直径的平均值和中位数.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】甲、乙两人练习罚球,每人练习6组,每组罚球20个,命中个数茎叶图如下:

(1)求甲命中个数的中位数和乙命中个数的众数;
(2)通过计算,比较甲乙两人的罚球水平.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的两个焦点为
的两个焦点为![]() ,
,![]() ,离心率为
,离心率为![]() ,点
,点![]() ,
,![]() 在椭圆上,
在椭圆上,![]() 在线段
在线段![]() 上,且
上,且![]() 的周长等于
的周长等于![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)过圆![]() 上任意一点
上任意一点![]() 作椭圆
作椭圆![]() 的两条切线
的两条切线![]() 和
和![]() 与圆
与圆![]() 交于点
交于点![]() ,
,![]() ,求
,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】袋中有外形、质量完全相同的红球、黑球、黄球、绿球共12个.从中任取一球,得到红球的概率是![]() ,得到黑球或黄球的概率是
,得到黑球或黄球的概率是![]() ,得到黄球或绿球的概率也是
,得到黄球或绿球的概率也是![]() .
.
(1)试分别求得到黑球、黄球、绿球的概率;
(2)从中任取一球,求得到的不是“红球或绿球”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解游客对2015年“十一”小长假的旅游情况是否满意,某旅行社从年龄在![]() 内的游客中随机抽取了1000人,并且作出了各个年龄段的频率直方图(如图所示),同时对这1000人的旅游结果满意情况进行统计得到下表:
内的游客中随机抽取了1000人,并且作出了各个年龄段的频率直方图(如图所示),同时对这1000人的旅游结果满意情况进行统计得到下表:

(1)求统计表中![]() 和
和![]() 的值;
的值;
(2)从年龄在![]() 内且对旅游结果满意的游客中,采用分层抽样的方法抽取10人,再从抽取的10人
内且对旅游结果满意的游客中,采用分层抽样的方法抽取10人,再从抽取的10人
中随机抽取4人做进一步调查,记4人中年龄在![]() 内的人数为
内的人数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校一个生物兴趣小组对学校的人工湖中养殖的某种鱼类进行观测研究,在饲料充足的前提下,兴趣小组对饲养时间x(单位:月)与这种鱼类的平均体重y(单位:千克)得到一组观测值,如下表:
|
|
|
|
|
|
|
|
|
|
|
|
(1)在给出的坐标系中,画出关于x、y两个相关变量的散点图.
(2)请根据上表提供的数据,用最小二乘法求出变量![]() 关于变量
关于变量![]() 的线性回归直线方程
的线性回归直线方程![]() .
.
(3)预测饲养满12个月时,这种鱼的平均体重(单位:千克).
(参考公式: 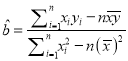 ,
, ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 为奇函数,(1)求
为奇函数,(1)求![]() 的值;(2)判断并证明函数
的值;(2)判断并证明函数![]() 的单调性;(3)是否存在这样的实数
的单调性;(3)是否存在这样的实数![]() ,使
,使![]() 对一切
对一切![]() 恒成立,若存在,试求出
恒成立,若存在,试求出![]() 取值的集合;若不存在,说明理由.
取值的集合;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com