
(本题满分14分)右图为一简单组合体,其底面ABCD为正方形,![]() 平面
平面![]() ,
,

![]() ,且
,且![]() , (1)求证:BE//平面PDA;
, (1)求证:BE//平面PDA;
(2)若N为线段![]() 的中点,求证:
的中点,求证:![]() 平面
平面![]() ;
;
(3)若![]() ,求平面PBE与平面ABCD所成的二面角的大小.
,求平面PBE与平面ABCD所成的二面角的大小.
(Ⅰ) 见解析 (Ⅱ) 见解析 (Ⅲ)45°--
(1)证明:∵![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]()
∴EC//平面![]() ,同理可得BC//平面
,同理可得BC//平面![]() ---------------2分
---------------2分
∵EC![]() 平面EBC,BC
平面EBC,BC![]() 平面EBC且
平面EBC且![]()
∴平面![]() //平面
//平面![]() ----------3分又∵BE
----------3分又∵BE![]() 平面EBC ∴BE//平面PDA---------4分
平面EBC ∴BE//平面PDA---------4分
(2)证法1:连结AC与BD交于点F, 连结NF,
∵F为BD的中点,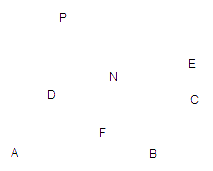 ∴
∴![]() 且
且![]() ,-------------6分
,-------------6分
又![]() 且
且![]()
∴![]() 且
且![]()
∴四边形NFCE为平行四边形-------------------------7分
∴![]()
∵![]()
![]() ,
,![]() 平面
平面![]() ,
,
![]() 面
面![]() ∴
∴![]() ,
,
又![]() ∴
∴![]() 面
面![]() ∴
∴![]() 面
面![]() --------------9分
--------------9分
[证法2:如图以点D为坐标原点,以AD所在的直线为x轴建立空间直角坐标系如图示:设该简单组合体的底面边长为1,![]()
 则
则![]()
![]() ,
,![]() --------------------------------6分
--------------------------------6分
∴![]() ,
,![]() ,
,![]()
∵![]() ,
,![]()
∴![]() -------------8分∵
-------------8分∵![]() 、
、![]() 面
面![]() ,且
,且![]()
∴![]() 面
面![]() ------9分
------9分
(3)解法1:连结DN,由(2)知![]() 面
面![]() ∴
∴![]() , ∵
, ∵![]() ,
, ![]()
∴![]() ∴
∴![]() ∴
∴![]() 为平面PBE的法向量,设
为平面PBE的法向量,设![]() ,则
,则![]()
∴![]() =
=![]() ---11分∵
---11分∵![]() 为平面ABCD的法向量,
为平面ABCD的法向量,![]() , --------12分
, --------12分
设平面PBE与平面ABCD所成的二面角为![]() ,则
,则![]() -----------13分
-----------13分
∴![]() 即平面PBE与平面ABCD所成的二面角为45°---------------------------------14分
即平面PBE与平面ABCD所成的二面角为45°---------------------------------14分
[解法2:延长PE与DC的延长线交于点G,连结GB,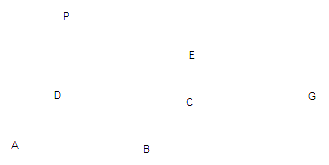 则GB为平面PBE与ABCD的交线-------10分
则GB为平面PBE与ABCD的交线-------10分
∵![]() ∴
∴![]()
∴D、B、G在以C为圆心、以BC为半径的圆上,
∴![]() -------------------11分
-------------------11分
∵![]() 平面
平面![]() ,
,![]() 面
面![]()
∴![]() 且
且![]()
∴![]() 面
面![]() ∵
∵![]() 面
面![]()
∴![]() ∴
∴![]() 为平面PBE与
为平面PBE与
平面ABCD所成的二面角的平面角--------13分
在![]() 中∵
中∵![]() ∴
∴![]() =45°即平面PBE与平面ABCD所成的二面角为45°-14分
=45°即平面PBE与平面ABCD所成的二面角为45°-14分
其它解法请参照给分


科目:高中数学 来源: 题型:
(本题满分14分)
右图为一简单组合体,其底面ABCD为正方形,![]() 平面
平面![]() ,
,
![]() ,且
,且![]() ,
,
(1)求证:BE//平面PDA;
(2)若N为线段![]() 的中点,求证:
的中点,求证:![]() 平面
平面![]() ;
;
 (3)若
(3)若![]() ,求平面PBE与平面ABCD所成的二面角的大小.
,求平面PBE与平面ABCD所成的二面角的大小.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年浙江省台州市高三上学期第三次统练文科数学 题型:解答题
(本题满分14分)右图为一简单组合体,其底面 为正方形,
为正方形,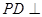 平面
平面 ,
, ,
,
且
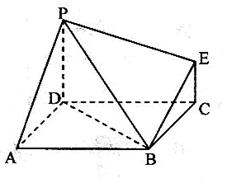
(1)求证: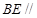 平面
平面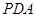 ;(2)求
;(2)求 与平面
与平面 所成角的大小.
所成角的大小.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年广东省高三上学期期中考试数学文卷 题型:解答题
((本题满分14分)右图为一简单集合体,其底面ABCD为正方形, 平面
平面 ,
,
 ,且
,且 =2 .
=2 .
(1)画出该几何体的三视图;
(2)求四棱锥B-CEPD的体积;
(3)求证: 平面
平面 .
.
查看答案和解析>>
科目:高中数学 来源:广州省2009-2010学年高二学科竞赛(数学文) 题型:解答题
(本题满分14分)右图为一简单组合体,其底面ABCD为正方形, 平面
平面 ,
,
 ,且
,且 =2 .
=2 .
(1)求四棱锥B-CEPD的体积;
(2)求证: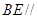 平面
平面 .
.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com