
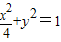 的两个焦点,点P在椭圆上,且△F1PF2的面积为1,则
的两个焦点,点P在椭圆上,且△F1PF2的面积为1,则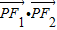 的值为( )
的值为( )
科目:高中数学 来源: 题型:
A.钝角三角形 B.锐角三角形
C.斜三角形 D.直角三角形
查看答案和解析>>
科目:高中数学 来源: 题型:
(本题20分,第1小题满分4分,第2小题满分6分,第3小题6分,第4小题4分)
我们知道,判断直线与圆的位置关系可以用圆心到直线的距离进行判别,那么直线与椭圆的位置关系有类似的判别方法吗?请同学们进行研究并完成下面问题。
(1)设F1、F2是椭圆![]() 的两个焦点,点F1、F2到直线
的两个焦点,点F1、F2到直线![]() 的距离分别为d1、d2,试求d1·d2的值,并判断直线L与椭圆M的位置关系。
的距离分别为d1、d2,试求d1·d2的值,并判断直线L与椭圆M的位置关系。
(2)设F1、F2是椭圆![]() 的两个焦点,点F1、F2到直线
的两个焦点,点F1、F2到直线 ![]() (m、n不同时为0)的距离分别为d1、d2,且直线L与椭圆M相切,试求d1·d2的值。
(m、n不同时为0)的距离分别为d1、d2,且直线L与椭圆M相切,试求d1·d2的值。
(3)试写出一个能判断直线与椭圆的位置关系的充要条件,并证明。
(4)将(3)中得出的结论类比到其它曲线,请同学们给出自己研究的有关结论(不必证明)。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com