
(本题12分)某人承揽一项业务,需做文字标牌4个,绘画标牌5个,现有两种规格的原料,甲种规格每张3m2,可做文字标牌1个,绘画标牌2个,乙种规格每张2m2,可做文字标牌2个,绘画标牌1个,求两种规格的原料各用多少张,才能使总的用料面积最小?

 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
(本小题满分12分)
某人向一目射击4次,每次击中目标的概率为![]() 。该目标分为3个不同的部分,第一、二、三部分面积之比为1:3:6。击中目标时,击中任何一部分的概率与其面积成正比。
。该目标分为3个不同的部分,第一、二、三部分面积之比为1:3:6。击中目标时,击中任何一部分的概率与其面积成正比。
(Ⅰ)设X表示目标被击中的次数,求X的分布列;
(Ⅱ)若目标被击中2次,A表示事件“第一部分至少被击中1次或第二部分被击中2次”,求P(A) ![]()
![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
(2009辽宁卷理)(本小题满分12分)
某人向一目射击4次,每次击中目标的概率为![]() 。该目标分为3个不同的部分,第一、二、三部分面积之比为1:3:6。击中目标时,击中任何一部分的概率与其面积成正比。
。该目标分为3个不同的部分,第一、二、三部分面积之比为1:3:6。击中目标时,击中任何一部分的概率与其面积成正比。
(Ⅰ)设X表示目标被击中的次数,求X的分布列;
(Ⅱ)若目标被击中2次,A表示事件“第一部分至少被击中1次或第二部分被击中2次”,求P(A) ![]()
![]()
查看答案和解析>>
科目:高中数学 来源:2011-2012学年甘肃省高三上学期期中考试理科数学试卷 题型:解答题
(本题12分)某人抛掷一枚硬币,出现正反的概率都是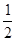 ,构造数列
,构造数列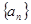 ,使
,使
得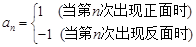 ,记
,记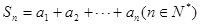 .
.
(Ⅰ)求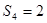 的概率;
的概率;
(Ⅱ)若前两次均出现正面,求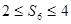 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题满分12分)
某人射击一次命中7~10环的概率如下表
| 命中环数 | 7 | 8 | 9 | 10 |
| 命中概率 | 0.16 | 0.19 | 0.28 | 0.24 |
计算这名射手在一次 射击中:
(1)射中9环或10环的概率;
(2)至少射中7环的概率;
(3)射中环数不足8环的概率
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com