
����Ŀ���ƻ���ijˮ�⽨һ�����లװ4̨�������ˮ��վ����ȥ50���ˮ��������ʾ��ˮ����������X������������һ����������ˮ�������ˮ֮�ͣ���λ���������ף�����40���ϣ����У�����80�������10�꣬������80�Ҳ���120�������30�꣬������120�Ҳ���160�������8�꣬������160�������2�꣬�����������������Ķε�Ƶ����Ϊ��Ӧ�εĸ��ʣ������������������������.
��1������δ��3���У�����1�����������������120�ĸ��ʣ�
��2��ˮ��վϣ����װ�ķ�������������У���ÿ�귢�����������̨������������X�����ƣ��������¹�ϵ��
��������X |
|
|
|
|
�������������̨�� | 1 | 2 | 3 | 4 |
��ij̨��������У����̨�����������Ϊ5000��Ԫ����ij̨�����δ���У����̨����������1500��Ԫ��ˮ��վ�ƻ��ڸ�ˮ�ⰲװ2̨��3̨�����������ΪӦ��װ2̨����3̨���������˵������.
���𰸡���1��![]() ����2��2̨�����ɼ�����
����2��2̨�����ɼ�����
��������
��1�����ö���ֲ����ʼ��㹫ʽ���������![]() �����������������
�����������������![]() �ĸ���.
�ĸ���.
��2���ֱ���ð�װ![]() ̨��
̨��![]() ̨����������������ֵ���ɴ�ȷ����װ��������̨��.
̨����������������ֵ���ɴ�ȷ����װ��������̨��.
��1�������⣺![]() ��
��![]() ��
��
![]() ��
��![]() .
.
������������������120�ĸ���Ϊ![]()
�ɶ���ֲ�����δ��3���У�����1�����������������120�ĸ���Ϊ��
![]() .
.
��2����ˮ��վ��������Ϊ![]() ����λ����Ԫ��
����λ����Ԫ��
������װ2̨����������Σ�
| 3500 | 10000 |
|
|
|
![]()
������װ3̨����������Σ�
| 2000 | 8500 | 15000 |
|
|
|
|
![]()
��Ϊ![]() ����Ӧ��װ2̨�����.
����Ӧ��װ2̨�����.


 ������ҵ����ν�����������ϵ�д�
������ҵ����ν�����������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס��ҡ������˲μ���Ⱥ�������Ϸ���������£�ÿ����Ϸ��![]() �������ÿ��������Ϊ
�������ÿ��������Ϊ![]() Ԫ��
Ԫ��![]() ����֪��ÿ����Ϸ����������
����֪��ÿ����Ϸ����������![]() ���������Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ��
���������Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ��
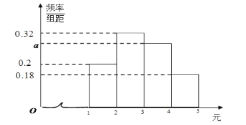
��1����![]() ��ֵ��������Ƶ�ʷֲ�ֱ��ͼ�����ƺ������������
��ֵ��������Ƶ�ʷֲ�ֱ��ͼ�����ƺ������������
��2����Ƶ�ʷֲ�ֱ��ͼ�е�Ƶ����Ϊ���ʣ����ס��ҡ������˴��и�����һ����������н����![]() �ĺ������Ϊ
�ĺ������Ϊ![]() ����
����![]() �ķֲ��к�������
�ķֲ��к�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijѧ���Ժ���![]() �����ʽ����о����ó����µĽ��ۣ�
�����ʽ����о����ó����µĽ��ۣ�
![]() ������
������![]() �ϵ����ݼ�����
�ϵ����ݼ�����![]() �ϵ���������
�ϵ���������
![]() ��
��![]() �Ǻ���ͼ���һ���Գ����ģ�
�Ǻ���ͼ���һ���Գ����ģ�
![]() ����ͼ�����ֱ��
����ͼ�����ֱ��![]() �Գƣ�
�Գƣ�
![]() ���ڳ���
���ڳ���![]() ��ʹ
��ʹ![]() ��һ��ʵ��x��������
��һ��ʵ��x��������
������ȷ����ĸ�����( )
A.1B.2C.3D.4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����и���������ȷ���������ǣ� ��
�� ����![]() ������������
������������![]() ��ż��������������ǡ�
��ż��������������ǡ�![]() ����ż������
����ż������![]() ��������������
��������������
�� ���⡰![]() ���ķ��ǡ�
���ķ��ǡ�![]() �� ��
�� ��
�� ������![]() ����С������Ϊ
����С������Ϊ![]() �� �ǡ�
�� �ǡ�![]() ���ı�Ҫ�����������
���ı�Ҫ�����������
�ܡ�ƽ������![]() ��
��![]() �ļн��Ƕ۽ǡ��ij�ֱ�Ҫ�����ǡ�
�ļн��Ƕ۽ǡ��ij�ֱ�Ҫ�����ǡ�![]() ��
��
A. �٢�B. �ۢ�C. �ڢ�D. �ڢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() .
.
��1������![]() �ĵ����ԣ�
�ĵ����ԣ�
��2���������![]() ����������ȵĽ�
����������ȵĽ�![]() ����
����![]() ��֤����
��֤����![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��![]() �У�
��![]() ��
��![]() ��
��![]() �ֱ�Ϊ
�ֱ�Ϊ![]() ��
��![]() �ߵ��е㣬��
�ߵ��е㣬��![]() Ϊ�ۺ۰�
Ϊ�ۺ۰�![]() ����ʹ��
����ʹ��![]() �����
�����![]() ��λ�ã���
��λ�ã���![]() ��
��
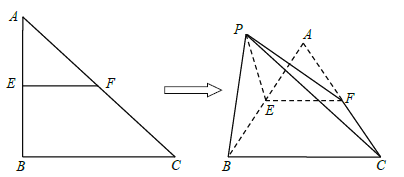
��1��֤����![]() ƽ��
ƽ��![]() ��
��
��2����ƽ��![]() ��ƽ��
��ƽ��![]() ���������ǵ�����ֵ��
���������ǵ�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������![]() �У�����
�У�����![]() �������Σ�
�������Σ�![]() �ǵ���ֱ�������Σ���
�ǵ���ֱ�������Σ���![]() ��������
��������![]() �Խ��ߵĽ���
�Խ��ߵĽ���![]() ��
��![]() ��
��![]() .
.

��1��֤����![]() ƽ��
ƽ��![]() ��
��
��2��������![]() �����
�����![]() ��ֱ����������
��ֱ����������![]() �����.
�����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x����|x+1|+2|x��m|
��1����m��2ʱ����f��x����9�Ľ⼯��
��2����f��x����2�Ľ⼯���ǿռ�����ʵ��m��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������![]() �У�����
�У�����![]() Ϊ���Σ�
���� ![]() ����
����![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ����
����

��1����֤��ƽ��![]()
![]() ƽ��
ƽ��![]() ��
��
��2����![]() Ϊ
Ϊ![]() �ϵ�һ�㣬����
�ϵ�һ�㣬����![]() ����ֱ��
����ֱ��![]() ��ƽ��
��ƽ��![]() ���ɽǵ�����ֵΪ
���ɽǵ�����ֵΪ![]() ��������
��������![]() ������ֵ��
������ֵ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com