
【题目】已知椭圆E:![]() +
+![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为![]() ,焦点到相应准线的距离为
,焦点到相应准线的距离为![]() .
.
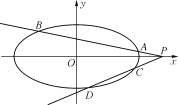
(1) 求椭圆E的标准方程;
(2) 已知P(t,0)为椭圆E外一动点,过点P分别作直线l1和l2,直线l1和l2分别交椭圆E于点A,B和点C,D,且l1和l2的斜率分别为定值k1和k2,求证:![]() 为定值.
为定值.
【答案】(1)![]() +y2=1;(2)证明见解析
+y2=1;(2)证明见解析
【解析】
(1)题中已知条件为![]() =
=![]() ,则
,则![]() -c=
-c=![]() ,结合
,结合![]() 可求得椭圆标准方程;
可求得椭圆标准方程;
(2)设A(x1,y1),B(x2,y2),设直线l1的方程为y=k1(x-t),代入椭圆E的方程中,并化简,应用韦达定理得![]() ,代入
,代入![]() 化简,同理得
化简,同理得![]() ,作比值
,作比值![]() 可得定值.
可得定值.
(1)设椭圆的半焦距为c,由已知得,
![]() =
=![]() ,则
,则![]() -c=
-c=![]() ,c2=a2-b2,
,c2=a2-b2,
解得a=2,b=1,c=![]() ,
,
所以椭圆E的标准方程是![]() +y2=1.
+y2=1.
(2) 由题意,设直线l1的方程为y=k1(x-t),代入椭圆E的方程中,并化简得
(1+4![]() )x2-8
)x2-8![]() tx+4
tx+4![]() t2-4=0,
t2-4=0,
设A(x1,y1),B(x2,y2).
则x1+x2=![]() ,x1x2=
,x1x2=![]() ,
,
因为PA=![]() |x1-t|,PB=
|x1-t|,PB=![]() |x2-t|,
|x2-t|,
所以PA·PB=(1+![]() )|x1-t||x2-t|=(1+
)|x1-t||x2-t|=(1+![]() )|t2-(x1+x2)t+x1x2|
)|t2-(x1+x2)t+x1x2|
=(1+![]() )|t2-
)|t2-![]() +
+![]() |=
|=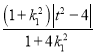 ,
,
同理,PC·PD=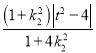 ,
,
所以![]() =
=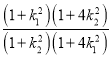 为定值.
为定值.


科目:高中数学 来源: 题型:
【题目】在数列{an}中,若an2﹣an﹣12=p,(n≥2,n∈N*,p为常数),则称{an}为“等方差数列”,下列是对“等方差数列“的判断:
①若{an}是等方差数列,则{an2}是等差数列;
②{(﹣1)n}是等方差数列;
③若{an}是等方差数列,则{akn}(k∈N*,k为常数)也是等方差数列;
④若{an}既是等方差数列,又是等差数列,则该数列为常数列.
其中正确命题的个数是( )
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位响应党中央“精准扶贫”号召,对某村6户贫困户中的甲户进行定点帮扶,每年跟踪调查统计一次,从2015年1月1日至2018年12月底统计数据如下(人均年纯收入):
年份 | 2015年 | 2016年 | 2017年 | 2018年 |
年份代码 | 1 | 2 | 3 | 4 |
收入 | 25 | 28 | 32 | 35 |
(1)请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ,并估计甲户在2019年能否脱贫;(国家规定2019年脱贫标准:人均年纯收入为3747元)
,并估计甲户在2019年能否脱贫;(国家规定2019年脱贫标准:人均年纯收入为3747元)
(2)2019年初,根据扶贫办的统计知,该村剩余5户贫困户中还有2户没有脱贫,现从这5户中抽取2户,求至少有一户没有脱贫的概率.
参考公式: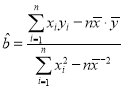 ,
,![]() ,其中
,其中![]() ,
,![]() 为数
为数![]() ,
,![]() 的平均数.
的平均数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知下列各命题:
①两两相交且不共点的三条直线确定一个平面:
②若真线![]() 不平行于平面
不平行于平面![]() ,则直线
,则直线![]() 与平面
与平面![]() 有公共点:
有公共点:
③若两个平面垂直,则一个平面内的已知直线必垂直于另一个平面的无数条直线:
④若两个二面角的两个面分别对应垂直,则这两个二面角相等或互补.
则其中正确的命题共有( )个
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,已知焦点在x轴上,离心率为![]() 的椭圆E的左顶点为A,点A到右准线的距离为6.
的椭圆E的左顶点为A,点A到右准线的距离为6.
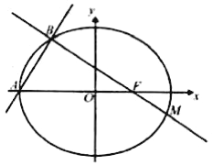
(1)求椭圆E的标准方程;
(2)过点A且斜率为![]() 的直线与椭圆E交于点B,过点B与右焦点F的直线交椭圆E于M点,求M点的坐标.
的直线与椭圆E交于点B,过点B与右焦点F的直线交椭圆E于M点,求M点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年底,湖北省武汉市等多个地区陆续出现感染新型冠状病毒肺炎的患者.为及时有效地对疫情数据进行流行病学统计分析,某地研究机构针对该地实际情况,根据该地患者是否有武汉旅行史与是否有确诊病例接触史,将新冠肺炎患者分为四类:有武汉旅行史(无接触史),无武汉旅行史(无接触史),有武汉旅行史(有接触史)和无武汉旅行史(有接触史),统计得到以下相关数据.
(1)请将列联表填写完整:
有接触史 | 无接触史 | 总计 | |
有武汉旅行史 | 27 | ||
无武汉旅行史 | 18 | ||
总计 | 27 | 54 |
(2)能否在犯错误的概率不超过0.025的前提下认为有武汉旅行史与有确诊病例接触史有关系?
附:![]()
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() 是定义域为R的奇函数.
是定义域为R的奇函数.
(1)求实数k的值;
(2)若![]() ,试判断函数
,试判断函数![]() 的单调性,并求不等式
的单调性,并求不等式![]() 的解集;
的解集;
(3)若![]() ,设
,设![]() ,
,![]() 在
在![]() 上的最小值为-1,求实数m的值.
上的最小值为-1,求实数m的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() ,阅读如图所示的程序框图,若输入的
,阅读如图所示的程序框图,若输入的![]() 的值为
的值为![]() ,输出的
,输出的![]() 的值恰为直线
的值恰为直线![]() 在
在![]() 轴上的截距,且
轴上的截距,且![]() .
.

(1)求直线![]() 与
与![]() 的交点坐标;
的交点坐标;
(2)若直线![]() 过直线
过直线![]() 与
与![]() 的交点,且在
的交点,且在![]() 轴上的截距是在
轴上的截距是在![]() 轴上的截距的2倍,求
轴上的截距的2倍,求![]() 的方程.
的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com