解:(1)设椭圆的标准方程为mx
2+ny
2=1,依题意可得
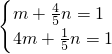
,可得

,
所以,所求椭圆的标准方程为

.(3分)
因为圆的圆心C和椭圆的右焦点重合,圆的半径恰为椭圆的短半轴长,
故园的标准方程为(x-2)
2+y
2=1.(5分)
(2)由(1)得圆心C(1,2),所以,而x
2+y
2-4x+3=0,则
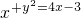
,
所以
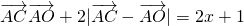
,(7分)
而(x-2)
2+y
2=1,则(x-2)
2≤1,即-1≤x-2≤1,即1≤x≤3,
因此,从而
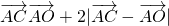
(O为坐标原点)的取值范围为[3,7].(10分)
(3)x
2+y
2表示圆上点P(x,y)与坐标原点O的距离的平方,因为原点O到圆心C(2,0)的距离为2,
圆的半径为1,所以P(x,y)与坐标原点O的距离的最小值为2-1=1,
与坐标原点O的距离的最大值为2+1=3,故x
2+y
2的最大值为9,最小值1.(14分)
分析:(1)设椭圆的标准方程为mx
2+ny
2=1,依题意可得
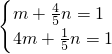
,由此能求出椭圆的标准方程和圆的标准方程.
(2)由圆心C(1,2),知x
2+y
2=4x-3,所以
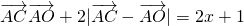
,而(x-2)
2+y
2=1,则1≤x≤3,由此能求出
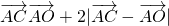
的取值范围.
(3)x
2+y
2表示圆上点P(x,y)与坐标原点O的距离的平方,因为原点O到圆心C(2,0)的距离为2,圆的半径为1,由此能求出x
2+y
2的最大值和最小值.
点评:本题主要考查直线与圆锥曲线的综合应用能力,具体涉及到轨迹方程的求法及直线与椭圆的相关知识,解题时要注意合理地进行等价转化.

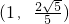 ,N
,N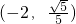 ,若圆C的圆心与椭圆的右焦点重合,圆的半径恰好等于椭圆的短半轴长,已知点A(x,y)为圆C上的一点.
,若圆C的圆心与椭圆的右焦点重合,圆的半径恰好等于椭圆的短半轴长,已知点A(x,y)为圆C上的一点.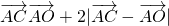 (O为坐标原点)的取值范围;
(O为坐标原点)的取值范围;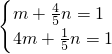 ,可得
,可得 ,
, .(3分)
.(3分)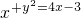 ,
,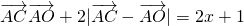 ,(7分)
,(7分)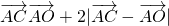 (O为坐标原点)的取值范围为[3,7].(10分)
(O为坐标原点)的取值范围为[3,7].(10分)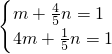 ,由此能求出椭圆的标准方程和圆的标准方程.
,由此能求出椭圆的标准方程和圆的标准方程.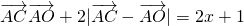 ,而(x-2)2+y2=1,则1≤x≤3,由此能求出
,而(x-2)2+y2=1,则1≤x≤3,由此能求出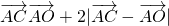 的取值范围.
的取值范围.

 阅读快车系列答案
阅读快车系列答案 已知椭圆的中心在坐标原点O,焦点在x轴上,短轴长为2,且两个焦点和短轴的两个端点恰为一个正方形的顶点.过右焦点F与x轴不垂直的直线l交椭圆于P,Q两点.
已知椭圆的中心在坐标原点O,焦点在x轴上,短轴长为2,且两个焦点和短轴的两个端点恰为一个正方形的顶点.过右焦点F与x轴不垂直的直线l交椭圆于P,Q两点.