
| A. | 最小正周期为π | |
| B. | 函数y=sin2x向左平移$\frac{π}{12}$个单位可得到f(x) | |
| C. | f(x)在区间$(-\frac{π}{3},\frac{π}{6})$上递增 | |
| D. | 点$(\frac{π}{6},0)$是f(x)的一个对称中心 |
分析 利用二倍角公式化简函数的解析式,然后判断选项的正误.
解答 解:函数f(x)=$\sqrt{3}sinxcosx+{cos}^{2}x-\frac{1}{2}$=$\frac{\sqrt{3}}{2}sin2x+\frac{1}{2}cos2x$=sin(2x+$\frac{π}{6}$).
函数的周期为:π,A正确;
函数y=sin2x向左平移$\frac{π}{12}$个单位可得到f(x)=sin2(x+$\frac{π}{12}$)=sin(2x+$\frac{π}{6}$),B正确;
由$-\frac{π}{2}<2x+\frac{π}{6}<\frac{π}{2}$,可得$-\frac{π}{3}<x<\frac{π}{6}$,f(x)在区间$(-\frac{π}{3},\frac{π}{6})$上递增,C正确;
x=$\frac{π}{6}$时,函数f(x)=1,点$(\frac{π}{6},0)$是f(x)的一个对称中心,不正确,D错误;
故选:D.
点评 本题考查二倍角公式以及两角和的正弦函数的应用,正弦函数的解得性质的应用,考查计算能力.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
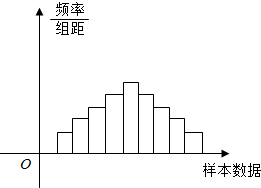 在样本的频率分布直方图中,共有9个小长方形,若第一个长方形的面积为0.04,前五个与后五个长方形的面积分别成等差数列且公差是互为相反数,若样本容量为800,则中间一组(即第五组)的频数为160.
在样本的频率分布直方图中,共有9个小长方形,若第一个长方形的面积为0.04,前五个与后五个长方形的面积分别成等差数列且公差是互为相反数,若样本容量为800,则中间一组(即第五组)的频数为160.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 | A规格 | B规格 | C规格 |
| 第一种钢板 | 2 | 1 | 1 |
| 第二种钢板 | 1 | 2 | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a<b<c | B. | b<a<c | C. | c<a<b | D. | c<b<a |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com