
【题目】对于函数f(x)=(|x﹣2|+1)4,给出如下三个命题:①f(x+2)是偶函数;②f(x)在区间(﹣∞,2)上是减函数,在区间(2,+∞)上是增函数;③f(x)没有最小值.其中正确的个数为( )
A. 1 B. 2 C. 3 D. 0
【答案】B
【解析】
由函数奇偶性的定义可判断①正确;讨论x>2,x<2,可以去掉绝对值,求得f(x),再利用复合函数判定单调性,即可判断②正确;由f(x)的单调性可判断③错误。
函数f(x)=(|x﹣2|+1)4,
设g(x)=f(x+2)=(|x|+1)4,
g(x)定义域为R,且g(﹣x)=g(x),可得g(x)是偶函数,故①正确;
x>2时,f(x)=(x﹣1)4,令![]() =(x﹣1)2则
=(x﹣1)2则![]() ,
,![]() ,
,
![]() =(x﹣1)2在x>2时单调递增,且
=(x﹣1)2在x>2时单调递增,且![]() 在
在![]() 时单调递增,所以x>2时,f(x)=(x﹣1)4 单调递增;
时单调递增,所以x>2时,f(x)=(x﹣1)4 单调递增;
x<2时,f(x)=(3﹣x)4,令![]() =(3﹣x)2则
=(3﹣x)2则![]() ,
,![]() ,
,
t=(3﹣x)2在x<2时单调递减,且![]() 在
在![]() 时单调递增,所以x<2时,f(x)=(3﹣x)4单调递减。故②正确;
时单调递增,所以x<2时,f(x)=(3﹣x)4单调递减。故②正确;
由②可得f(x)在x=2处取得最小值1,故③错误.
故选:B.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】![]() 是双曲线
是双曲线![]() 上一点,
上一点, ![]() 分别是双曲线
分别是双曲线![]() 的左、右顶点,直线
的左、右顶点,直线![]() 的斜率之积为
的斜率之积为![]() .
.
(1)求双曲线的离心率;
(2)过双曲线![]() 的右焦点且斜率为
的右焦点且斜率为![]() 的直线交双曲线于
的直线交双曲线于![]() 两点,
两点, ![]() 为坐标原点,
为坐标原点, ![]() 为双曲线上一点,满足
为双曲线上一点,满足![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解少年儿童的肥胖是否与常喝碳酸饮料有关,现对![]() 名小学六年级学生进行了问卷调查,并得到如下列联表.平均每天喝
名小学六年级学生进行了问卷调查,并得到如下列联表.平均每天喝![]() 以上为“常喝”,体重超过
以上为“常喝”,体重超过![]() 为“肥胖”.
为“肥胖”.
常喝 | 不常喝 | 合计 | |
肥胖 | 2 | ||
不肥胖 | 18 | ||
合计 | 30 |
已知在全部![]() 人中随机抽取
人中随机抽取![]() 人,抽到肥胖的学生的概率为
人,抽到肥胖的学生的概率为![]() .
.
(1)请将上面的列联表补充完整;
(2)是否有![]() 的把握认为肥胖与常喝碳酸饮料有关?请说明你的理由;
的把握认为肥胖与常喝碳酸饮料有关?请说明你的理由;
(3)已知常喝碳酸饮料且肥胖的学生中恰有2名女生,现从常喝碳酸饮料且肥胖的学生中随机抽取2人参加一个有关健康饮食的电视节目,求恰好抽到一名男生和一名女生的概率.
附:![]()
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】提高过江大桥的车辆通行能力可改善整个城市的交通状况,在一般情况下,大桥上的车流速度v(单位:千米/小时)是车流密度x(单位:辆/千米)的函数,当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速度为60千米/小时,研究表明:当20≤x≤200时,车流速度v是车流密度x的一次函数.
(1)当0≤x≤200时,求函数v(x)的表达式;
(2)当车流密度x为多大时,车流量(单位时间内通过桥上某观测点的车辆数,单位:辆/小时)f(x)=xv(x)可以达到最大,并求出最大值.(精确到1辆/小时).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四面体ABCD中,△ABC是正三角形,AD=CD.
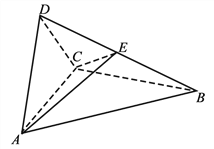
(1)证明:AC⊥BD;
(2)已知△ACD是直角三角形,AB=BD.若E为棱BD上与D不重合的点,且AE⊥EC,求四面体ABCE与四面体ACDE的体积比.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某粮库拟建一个储粮仓如图所示,其下部是高为2的圆柱,上部是母线长为2的圆锥,现要设计其底面半径和上部圆锥的高,若设圆锥的高![]() 为
为![]() ,储粮仓的体积为
,储粮仓的体积为![]() .
.
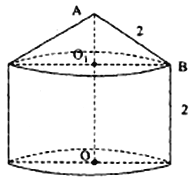
(1)求![]() 关于
关于![]() 的函数关系式;(圆周率用
的函数关系式;(圆周率用![]() 表示)
表示)
(2)求![]() 为何值时,储粮仓的体积最大.
为何值时,储粮仓的体积最大.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义域为R的偶函数f(x)满足对x∈R,有f(x+2)=f(x)﹣f(1),且当x∈[2,3]时,f(x)=﹣2x2+12x﹣18,若函数y=f(x)﹣loga(|x|+1)在(0,+∞)上至少有三个零点,则a的取值范围是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4﹣5:不等式选讲
已知函数f(x)=|x+1|﹣|x|+a.
(1)若a=0,求不等式f(x)≥0的解集;
(2)若方程f(x)=x有三个不同的解,求a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com