
【题目】已知椭圆E:![]() 的焦点在
的焦点在![]() 轴上,A是E的左顶点,斜率为k (k > 0)的直线交E于A,M两点,点N在E上,MA⊥NA.
轴上,A是E的左顶点,斜率为k (k > 0)的直线交E于A,M两点,点N在E上,MA⊥NA.
(Ⅰ)当t=4,![]() 时,求△AMN的面积;
时,求△AMN的面积;
(Ⅱ)当![]() 时,求k的取值范围.
时,求k的取值范围.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】某地区高考实行新方案,规定:语文、数学和英语是考生的必考科目,考生还须从物理、化学、生物、历史、地理和政治六个科目中选取三个科目作为选考科目,若一名学生从六个科目中选出了三个科目作为选考科目,则称该学生的选考方案确定;否则,称该学生选考方案待确定.例如,学生甲选择“物理、化学和生物”三个选考科目,则学生甲的选考方案确定,“物理、化学和生物”为其选考方案.
某学校为了了解高一年级420名学生选考科目的意向,随机选取30名学生进行了一次调查,统计选考科目人数如下表:
性别 | 选考方案确定情况 | 物理 | 化学 | 生物 | 历史 | 地理 | 政治 |
男生 | 选考方案确定的有8人 | 8 | 8 | 4 | 2 | 1 | 1 |
选考方案待确定的有6人 | 4 | 3 | 0 | 1 | 0 | 0 | |
女生 | 选考方案确定的有10人 | 8 | 9 | 6 | 3 | 3 | 1 |
选考方案待确定的有6人 | 5 | 4 | 1 | 0 | 0 | 1 |
(Ⅰ)估计该学校高一年级选考方案确定的学生中选考生物的学生有多少人?
(Ⅱ)假设男生、女生选择选考科目是相互独立的.从选考方案确定的8位男生随机选出1人,从选考方案确定的10位女生中随机选出1人,试求该男生和该女生的选考方案中都含有历史科目的概率;
(Ⅲ)从选考方案确定的8名男生随机选出2名,设随机变量两名男生选考方案相同时![]() ,两名男生选考方案不同时
,两名男生选考方案不同时![]() ,求
,求![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,已知圆![]() 的方程为
的方程为![]() ,圆
,圆![]() 的方程为
的方程为![]() ,动圆
,动圆![]() 与圆
与圆![]() 内切且与圆
内切且与圆![]() 外切.
外切.
(1)求动圆圆心![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)已知![]() 与
与![]() 为平面内的两个定点,过
为平面内的两个定点,过![]() 点的直线
点的直线![]() 与轨迹
与轨迹![]() 交于
交于![]() ,
,![]() 两点,求四边形
两点,求四边形![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】进入12月以来,某地区为了防止出现重污染天气,坚持保民生、保蓝天,严格落实机动车限行等一系列“管控令”.该地区交通管理部门为了了解市民对“单双号限行”的赞同情况,随机采访了220名市民,将他们的意见和是否拥有私家车情况进行了统计,得到如下的![]() 列联表:
列联表:
赞同限行 | 不赞同限行 | 合计 | |
没有私家车 | 90 | 20 | 110 |
有私家车 | 70 | 40 | 110 |
合计 | 160 | 60 | 220 |
(1)根据上面的列联表判断,能否在犯错误的概率不超过0.001的前提下认为“是否赞同限行与是否拥有私家车”有关;
(2)为了了解限行之后是否对交通拥堵、环境污染起到改善作用,从上述调查的不赞同限行的人员中按分层抽样抽取6人,再从这6人中随机抽出3名进行电话回访,求3人中至少抽到1名“没有私家车”人员的概率.
附:![]() .
.
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高三理科班共有60名同学参加某次考试,从中随机挑选出5名同学,他们的数学成绩![]() 与物理成绩
与物理成绩![]() 如下表:
如下表:

数据表明![]() 与
与![]() 之间有较强的线性关系.
之间有较强的线性关系.
(1)求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)该班一名同学的数学成绩为110分,利用(1)中的回归方程,估计该同学的物理成绩;
(3)本次考试中,规定数学成绩达到125分为优秀,物理成绩达到100分为优秀.若该班数学优秀率与物理优秀率分别为![]() 和
和![]() ,且除去抽走的5名同学外,剩下的同学中数学优秀但物理不优秀的同学共有5人.能否在犯错误概率不超过0.01的前提下认为数学优秀与物理优秀有关?
,且除去抽走的5名同学外,剩下的同学中数学优秀但物理不优秀的同学共有5人.能否在犯错误概率不超过0.01的前提下认为数学优秀与物理优秀有关?
参考数据:回归直线的系数 ,
,![]() .
.
![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】用适当的方法表示下列集合:
(1)一年中有31天的月份的全体;
(2)大于![]() 小于12.8的整数的全体;
小于12.8的整数的全体;
(3)梯形的全体构成的集合;
(4)所有能被3整除的数的集合;
(5)方程![]() 的解组成的集合;
的解组成的集合;
(6)不等式![]() 的解集.
的解集.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】大连市某企业为确定下一年投入某种产品的宣传费,需了解年宣传费![]() (单位:千元)对年销售量
(单位:千元)对年销售量![]() (单位:
(单位:![]() )和年利润
)和年利润![]() (单位:千元)的影响,对近8年的年宣传费
(单位:千元)的影响,对近8年的年宣传费![]() 和年销售量
和年销售量![]() 数据作了初步处理,得到下面的散点图及一些统计量的值.
数据作了初步处理,得到下面的散点图及一些统计量的值.

|
|
|
|
|
|
|
46.6 | 573 | 6.8 | 289.8 | 1.6 | 215083.4 | 31280 |
表中![]() ,
,![]() .
.
根据散点图判断,
![]() 与
与![]() 哪一个适宜作为年销售量
哪一个适宜作为年销售量![]() 关于年宣传费
关于年宣传费![]() 的回归方程类型?(给出判断即可,不必说明理由)
的回归方程类型?(给出判断即可,不必说明理由)
![]() 根据
根据![]() 的判断结果及表中数据,建立
的判断结果及表中数据,建立![]() 关于
关于![]() 的回归方程;
的回归方程;
![]() 已知这种产品的年利润
已知这种产品的年利润![]() 与
与![]() 、
、![]() 的关系为
的关系为![]() .根据
.根据![]() 的结果回答下列问题:
的结果回答下列问题:
![]() 年宣传费
年宣传费![]() 时,年销售量及年利润的预报值是多少?
时,年销售量及年利润的预报值是多少?
![]() 年宣传费
年宣传费![]() 为何值时,年利润的预报值最大?
为何值时,年利润的预报值最大?
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为:
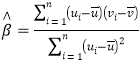 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的一个焦点与抛物线
的一个焦点与抛物线![]() 的焦点
的焦点![]() 重合,且椭圆短轴的两个端点与点
重合,且椭圆短轴的两个端点与点![]() 构成正三角形.
构成正三角形.
(1)求椭圆的方程;
(2)若过点![]() 的直线
的直线![]() 与椭圆交于不同的两点
与椭圆交于不同的两点![]() ,试问在
,试问在![]() 轴上是否存在定点
轴上是否存在定点![]() ,使
,使![]() 恒为定值?若存在,求出
恒为定值?若存在,求出![]() 的坐标,并求出这个定值;若不存在,请说明理由.
的坐标,并求出这个定值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com