练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】在直角坐标系中，以原点为极点，x轴的正半轴为极轴建立极坐标系，已知曲线C： ，过点的直线l的参数方程为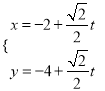： (t为参数)，直线l与曲线C分别交于M、N两点．

    (Ⅰ)写出曲线C的直角坐标方程和直线l的普通方程；

    (Ⅱ)若| PM |，| MN |，| PN |成等比数列，求a的值．

    【答案】(Ⅰ) (a > 0)， (Ⅱ) ．

    【解析】试题分析：（1）利用把极坐标方程转化为直角方程．把直线中的参数消去即可得到其普通方程．（2）由直线方程中参数的几何意义可以得到，把直线的参数方程代入抛物线的普通方程得到满足的方程，利用韦达定理把转化为关于的方程，求出即可．

    解析：（Ⅰ）解：由 得： ，∴曲线的直角坐标方程为： ，由 消去参数得直线的普通方程为．

    （Ⅱ）解：将直线l的参数方程 代入中得： ，设两点对应的参数分别为，则有 , ， ， ，即 ，解得．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知函数定义在上，且可以表示为一个偶函数与一个奇函数之和，设，

    （1）求出的解析式；

    （2）若对于任意恒成立，求的取值范围；

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设公差大于0的等差数列{an}的前n项和为Sn，已知S3=15，且a1，a4，a13成等比数列，记数列 的前n项和为Tn．

    （Ⅰ）求Tn；

    （Ⅱ）若对于任意的n∈N*，tTn＜an+11恒成立，求实数t的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数

    （1）当时，求函数的单调区间．

    （2）当且时，不等式在上恒成立，求k的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某学校400名学生在一次百米赛跑测试中，成绩全部都在12秒到17秒之间，现抽取其中50个样本，将测试结果按如下方式分成五组：第一组，第二组，…，第五组，如图所示的是按上述分组方法得到的频率分布直方图．

    （1）请估计该校400名学生中，成绩属于第三组的人数；

    （2）请估计样本数据的中位数（精确到0.01）；

    （3）若样本第一组中只有一名女生，其他都是男生，第五组则只有一名男生，其他都是女生，现从第一、第五组中各抽取2名同学组成一个特色组，设其中男同学的人数为，求的分布列和期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】通过随机询问110名大学生是否爱好某项运动，得到列联表：

    男

    女

    总计

    爱好

    40

    20

    60

    不爱好

    20

    30

    50

    总计

    60

    50

    110

    由K2＝，得K2＝≈7.8.

    附表：

    P(K2≥k0)

    0.050

    0.010

    0.001

    k0

    3.841

    6.635

    10.828

    参照附表，得到的正确结论是(　　)

    A. 有99%以上的把握认为“爱好该项运动与性别有关”

    B. 有99%以上的把握认为“爱好该项运动与性别无关”

    C. 在犯错误的概率不超过0.1%的前提下，认为“爱好该项运动与性别有关”

    D. 在犯错误的概率不超过0.1%的前提下，认为“爱好该项运动与性别无关”

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】为了了解某校九年级1 600名学生的体能情况，随机抽查了部分学生，测试1分钟仰卧起坐的成绩(次数)，将数据整理后绘制成如图所示的频率分布直方图，根据直方图的数据，下列结论错误的是(　　)

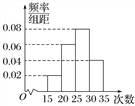
    A. 该校九年级学生1分钟仰卧起坐的次数的中位数为26.25

    B. 该校九年级学生1分钟仰卧起坐的次数的众数为27.5

    C. 该校九年级学生1分钟仰卧起坐的次数超过30次的约有320人

    D. 该校九年级学生1分钟仰卧起坐的次数少于20次的约有32人

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】“扶贫帮困”是中华民族的传统美德，某校为帮扶困难同学，采用如下方式进行一次募捐：在不透明的箱子中放入大小均相同的白球七个，红球三个，每位献爱心的参与者投币20元有一次摸奖机会，一次性从箱子中摸球三个（摸完球后将球放回），若有一个红球，奖金10元，两个红球奖金20元，三个全是红球奖金100元.

    （1）求献爱心参与者中将的概率；

    （2）若该次募捐900位献爱心参与者，求此次募捐所得善款的数学期望.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆的左、右焦点分别为F1(－c，0)，F2(c，0)，直线交椭圆E于A，B两点，△ABF1的周长为16，△AF1F2的周长为12．

    (1)求椭圆E的标准方程与离心率；

    (2)若直线l与椭圆E交于C，D两点，且P(2，2)是线段CD的中点，求直线l的一般方程．

    查看答案和解析>>

    同步练习册答案