
分析 (1)当k=1时,求出导数f′(x),求得切线的斜率和切点,可得切线的方程;
(2)求出h(x)的导数,讨论k的范围,分k≥1,$\frac{1}{2}$<k<1,由导数大于0,可得增区间;由导数小于0,可得减区间;
(3)由g′(x0)=$\frac{{g({x_1})-g({x_2})}}{{{x_1}-{x_2}}}$,可得lnx0+1=$\frac{{x}_{1}ln{x}_{1}-{x}_{2}ln{x}_{2}}{{x}_{1}-{x}_{2}}$,进而可变形为lnx0-lnx1=$\frac{ln\frac{{x}_{1}}{{x}_{2}}+1-\frac{{x}_{1}}{{x}_{2}}}{\frac{{x}_{1}}{{x}_{2}}-1}$,只需证明lnx0-lnx1>0,设φ(t)=lnt+1-t,其中0<t<1,用导数可判断φ(t)<φ(1)=0,又$\frac{{x}_{1}}{{x}_{2}}$-1<0,可得结论.
解答 解:(1)当k=1时,函数f(x)=lnx+$\frac{1}{x}$,
则f′(x)=$\frac{1}{x}$-$\frac{1}{{x}^{2}}$=$\frac{x-1}{{x}^{2}}$,
即有在点(1,f(1))处的切线斜率为0,切点为(1,1),
可得在点(1,f(1))处的切线方程为y=1;
(2)若k>$\frac{1}{2}$,令h(x)=f(x)+(k-1)x=lnx+$\frac{k}{x}$+(k-1)x,
即有h′(x)=$\frac{1}{x}$-$\frac{k}{{x}^{2}}$+k-1=$\frac{(k-1){x}^{2}+x-k}{{x}^{2}}$=$\frac{(x-1)[(k-1)x+k]}{{x}^{2}}$,
当k≥1,即有(k-1)x+k>0,当h′(x)>0,可得x>1;当h′(x)<0,可得0<x<1;
当$\frac{1}{2}$<k<1,即有1<$\frac{k}{1-k}$,当h′(x)>0,可得$\frac{k}{1-k}$<x<1;
当h′(x)<0,可得x<$\frac{k}{1-k}$或x>1.
综上可得,k≥1,h(x)在(0,1)递减;在(1,+∞)递增;
当$\frac{1}{2}$<k<1时,f(x)在($\frac{k}{1-k}$,1)递增,在(-∞,$\frac{k}{1-k}$),(1,+∞)递减;
(3)g(x)=xf(x)-k=xlnx,g′(x)=lnx+1,
因为对任意的x1,x2(0<x1<x2),总存在x0>0,
使得g′(x0)=$\frac{{g({x_1})-g({x_2})}}{{{x_1}-{x_2}}}$成立,
所以lnx0+1=$\frac{{g({x_1})-g({x_2})}}{{{x_1}-{x_2}}}$,
即lnx0+1=$\frac{{x}_{1}ln{x}_{1}-{x}_{2}ln{x}_{2}}{{x}_{1}-{x}_{2}}$,
即lnx0-lnx1=$\frac{{x}_{1}ln{x}_{1}-{x}_{2}ln{x}_{2}}{{x}_{1}-{x}_{2}}$-1-lnx1
=$\frac{{x}_{2}ln{x}_{1}-{x}_{2}ln{x}_{2}+{x}_{2}-{x}_{1}}{{x}_{1}-{x}_{2}}$=$\frac{ln\frac{{x}_{1}}{{x}_{2}}+1-\frac{{x}_{1}}{{x}_{2}}}{\frac{{x}_{1}}{{x}_{2}}-1}$,
设t=$\frac{{x}_{1}}{{x}_{2}}$,(0<t<1),
则φ(t)=lnt+1-t,其中0<t<1,则φ′(t)=$\frac{1}{t}$-1>0,
因而φ(t)在区间(0,1)上单调递增,φ(t)<φ(1)=0,
又$\frac{{x}_{1}}{{x}_{2}}$-1<0,所以lnx0-lnx1>0,即x0>x1.
点评 本题考查利用导数研究函数的切线方程和单调性,考查分类讨论的思想方法,考查不等式的证明,注意运用构造法,运用函数的单调性,属于中档题..


科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 4 | C. | 6 | D. | 12 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
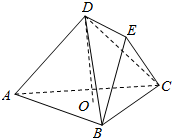 如图所示,在几何体ABCDE中,AB=BC=CA=EB=EC=2$\sqrt{3}$,DE=$\sqrt{2}$,点D在底面ABC上的射影O为底面三角形ABC的中心,平面BEC⊥平面ABC.
如图所示,在几何体ABCDE中,AB=BC=CA=EB=EC=2$\sqrt{3}$,DE=$\sqrt{2}$,点D在底面ABC上的射影O为底面三角形ABC的中心,平面BEC⊥平面ABC.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若“p∨q”为假命题,则p,q均为假命题 | |
| B. | “x=1”是“x≥1”的充分不必要条件 | |
| C. | “sinx=$\frac{1}{2}$”的必要不充分条件是“x=$\frac{π}{6}$” | |
| D. | 若命题p:?x0∈R,x02≥0,则命题¬p:?x∈R,x2<0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| x | -$\frac{π}{3}$ | -$\frac{π}{12}$ | 0 | $\frac{π}{6}$ | $\frac{5π}{12}$ | $\frac{2π}{3}$ | $\frac{11π}{12}$ |
| f(x) | -1 | 1 | 2 | 3 | 1 | -1 | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com