
【题目】在等差数列{an}中,a15+a16+a17=﹣45,a9=﹣36,Sn为其前n项和.
(1)求Sn的最小值,并求出相应的n值;
(2)求Tn=|a1|+|a2|+…+|an|.
【答案】
(1)解:等差数列{an}中,a15+a16+a17=﹣45,a9=﹣36,
∴3a1+45d=﹣45,a1+8d=﹣36,
解得a1=﹣60,d=3.
∴an=﹣60+3(n﹣1)=3n﹣63.
Sn= ![]() =
= ![]() .
.
令an=3n﹣63≤0.解得n≤21.
∴n=20或21时Sn取得最小值= ![]() =﹣630.
=﹣630.
(2)解:n≤21时,Tn=|a1|+|a2|+…+|an|=﹣(a1+a2+…+an)=﹣Sn.
n≥22时,Tn=|a1|+|a2|+…+|an|=﹣(a1+a2+…+a21)+a22+…+an=﹣2S21+Sn= ![]() ﹣2×(﹣630)=
﹣2×(﹣630)= ![]() +1260.
+1260.
【解析】(1)利用等差数列通项公式与求和公式即可得出.(2)n≤21时,Tn=|a1|+|a2|+…+|an|=﹣(a1+a2+…+an)=﹣Sn . n≥22时,Tn=|a1|+|a2|+…+|an|=﹣(a1+a2+…+a21)+a22+…+an=﹣2S21+Sn .


科目:高中数学 来源: 题型:
【题目】如图在四面体OABC中,OA,OB,OC两两垂直,且OB=OC=3,OA=4,给出如下判断: ①存在点D(O点除外),使得四面体DABC有三个面是直角三角形;
②存在点D,使得点O在四面体DABC外接球的球面上;
③存在唯一的点D使得OD⊥平面ABC;
④存在点D,使得四面体DABC是正棱锥;
⑤存在无数个点D,使得AD与BC垂直且相等.
其中正确命题的序号是(把你认为正确命题的序号填上).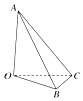
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知m,n,s,t∈R+ , m+n=2, ![]() +
+ ![]() =9,其中m,n是常数,当s+t取最小值
=9,其中m,n是常数,当s+t取最小值 ![]() 时,m,n对应的点(m,n)是椭圆
时,m,n对应的点(m,n)是椭圆 ![]() =1的一条弦的中点,则此弦所在的直线方程 .
=1的一条弦的中点,则此弦所在的直线方程 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题p:k2﹣8k﹣20≤0,命题q:方程 ![]() =1表示焦点在x轴上的双曲线. (Ⅰ)命题q为真命题,求实数k的取值范围;
=1表示焦点在x轴上的双曲线. (Ⅰ)命题q为真命题,求实数k的取值范围;
(Ⅱ)若命题“p∨q”为真,命题“p∧q”为假,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义域为[0,e]的函数f(x)同时满足: ①对于任意的x∈[0,e],总有f(x)≥0;
②f(e)=e;
③若x1≥0,x2≥0,x1+x2≤e,则恒有f(x1+x2)≥f(x1)+f(x2).
(1)求f(0)的值;
(2)证明:不等式f(x)≤e对任意x∈[0,e]恒成立;
(3)若对于任意x∈[0,e],总有4f2(x)﹣4(2e﹣a)f(x)+4e2﹣4ea+1≥0,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC﹣A1B1C1中,平面A1BC⊥侧面A1B1BA,且AA1=AB=BC=2,则AC与平面A1BC所成角为( ) 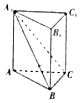
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com