
【题目】已知函数f(x)![]() x3+ax2+bx,且f′(﹣1)=0.
x3+ax2+bx,且f′(﹣1)=0.
(1)试用含a的代数式表示b;
(2)求f(x)的单调区间;
(3)令a=﹣1,设函数f(x)在x1、x2(x1<x2)处取得极值,记点M(x1,f(x1)),N(x2,f(x2)).证明:线段MN与曲线f(x)存在异于M,N的公共点.
【答案】(1)b=2a﹣1.(2)见解析(3)见解析
【解析】
(1)求导得到f′(x)=x2+2ax+b,代入数据计算得到答案.
(2)讨论a>1,a=1和a<1三种情况,分别计算得到答案.
(3)f′(x)=x2﹣2x﹣3=0,得x1=﹣1,x2=3,得到函数单调区间,得到MN的方程为y![]() x﹣1,计算F(0)=3>0,F(2)=﹣3<0,得到答案.
x﹣1,计算F(0)=3>0,F(2)=﹣3<0,得到答案.
(1)依题意,得f′(x)=x2+2ax+b.由f′(﹣1)=1﹣2a+b=0得b=2a﹣1.
(2)f(x)![]() x3+ax2+(2a﹣1)x,故f′(x)=x2+2ax+2a﹣1=(x+1)(x+2a﹣1).
x3+ax2+(2a﹣1)x,故f′(x)=x2+2ax+2a﹣1=(x+1)(x+2a﹣1).
令f′(x)=0,则x=﹣1或x=1﹣2a.
①当a>1时,1﹣2a<﹣1.
当x变化时,f′(x)与f(x)的变化情况如下表:
x | (﹣∞,1﹣2a) | (1﹣2a,﹣1) | (﹣1,+∞) |
f′(x) | + | ﹣ | + |
f(x) | 单调递增 | 单调递减 | 单调递增 |
得,函数f(x)的单调增区间为(﹣∞,1﹣2a)和(﹣1,+∞),单调减区间为(1﹣2a,﹣1).
②当a=1时,1﹣2a=﹣1.此时,f′(x)≥0恒成立,且仅在x=﹣1处f′(x)=0,故函数f(x)的单调增区间为(﹣∞,+∞).
③当a<1时,1﹣2a>﹣1,同理可得函数f(x)的单调增区间为(﹣∞,﹣1)和(1﹣2a,+∞),单调减区间为(﹣1,1﹣2a).
综上所述:当a>1时,函数f(x)的单调增区间为(﹣∞,1﹣2a)和(﹣1,+∞),单调减区间为(1﹣2a,﹣1);
当a=1时,函数f(x)的单调增区间为(﹣∞,+∞);
当a<1时,函数f(x)的单调增区间为(﹣∞,﹣1)和(1﹣2a,+∞),单调减区间为(﹣1,1﹣2a).
(3)当a=﹣1时,得f(x)![]() x3﹣x2﹣3x.
x3﹣x2﹣3x.
由f′(x)=x2﹣2x﹣3=0,得x1=﹣1,x2=3.
由(2)得f(x)的单调增区间为(﹣∞,﹣1)和(3,+∞),单调减区间为(﹣1,3),
所以函数f(x)在x1=﹣1,x2=3处取得极值.故M(﹣1,![]() ),N(3,﹣9).
),N(3,﹣9).
所以直线MN的方程为y![]() x﹣1.
x﹣1.
由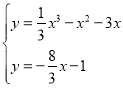 得x3﹣3x2﹣x+3=0.
得x3﹣3x2﹣x+3=0.
令F(x)=x3﹣3x2﹣x+3.
易得F(0)=3>0,F(2)=﹣3<0,而F(x)的图象在(0,2)内是一条连续不断的曲线,
故F(x)在(0,2)内存在零点x0,这表明线段MN与曲线f(x)有异于M,N的公共点.


 智能训练练测考系列答案
智能训练练测考系列答案科目:高中数学 来源: 题型:
【题目】(2017高考新课标Ⅲ,理19)如图,四面体ABCD中,△ABC是正三角形,△ACD是直角三角形,∠ABD=∠CBD,AB=BD.
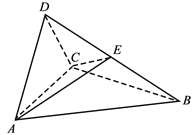
(1)证明:平面ACD⊥平面ABC;
(2)过AC的平面交BD于点E,若平面AEC把四面体ABCD分成体积相等的两部分,求二面角D–AE–C的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在衡阳市“创全国文明城市”(简称“创文”)活动中,市教育局对本市A,B,C,D四所高中学校按各校人数分层抽样,随机抽查了200人,将调查情况进行整理后制成下表:
学校 | A | B | C | D |
抽查人数 | 10 | 15 | 100 | 75 |
“创文”活动中参与的人数 | 9 | 10 | 80 | 49 |
假设每名高中学生是否参与“创文”活动是相互独立的
(1)若本市共8000名高中学生,估计C学校参与“创文”活动的人数;
(2)在上表中从A,B两校没有参与“创文”活动的同学中随机抽取2人,求恰好A,B两校各有1人没有参与“创文”活动的概率;
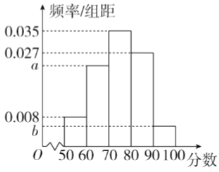
(3)在随机抽查的200名高中学生中,进行文明素养综合素质测评(满分为100分),得到如上的频率分布直方图,其中![]() .求a,b的值,并估计参与测评的学生得分的中位数.(计算结果保留两位小数).
.求a,b的值,并估计参与测评的学生得分的中位数.(计算结果保留两位小数).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学为了解高二年级中华传统文化经典阅读的整体情况,从高二年级随机抽取10名学生进行了两轮测试,并把两轮测试成绩的平均分作为该名学生的考核成绩.记录的数据如下:
1号 | 2号 | 3号 | 4号 | 5号 | 6号 | 7号 | 8号 | 9号 | 10号 | |
第一轮测试成绩 | 96 | 89 | 88 | 88 | 92 | 90 | 87 | 90 | 92 | 90 |
第二轮测试成绩 | 90 | 90 | 90 | 88 | 88 | 87 | 96 | 92 | 89 | 92 |
(Ⅰ)从该校高二年级随机选取一名学生,试估计这名学生考核成绩大于90 分的概率;
(Ⅱ)从考核成绩大于90分的学生中再随机抽取两名同学,求这两名同学两轮测试成绩均大于等于90分的概率;
(Ⅲ)记抽取的10名学生第一轮测试的平均数和方差分别为![]() ,
,![]() ,考核成绩的平均数和方差分别为
,考核成绩的平均数和方差分别为![]() ,
,![]() ,试比较
,试比较![]() 与
与![]() ,
, ![]() 与
与![]() 的大小.(只需写出结论)
的大小.(只需写出结论)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() 是定义为R的偶函数,且
是定义为R的偶函数,且![]() 对任意的
对任意的![]() ,都有
,都有![]() 且当
且当![]() 时,
时, ![]() ,若在区间
,若在区间![]() 内关于
内关于![]() 的方程
的方程![]() 恰好有3个不同的实数根,则
恰好有3个不同的实数根,则![]() 的取值范围是 ( )
的取值范围是 ( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,圆柱体木材的横截面半径为![]() ,从该木材中截取一段圆柱体,再加工制作成直四棱柱
,从该木材中截取一段圆柱体,再加工制作成直四棱柱![]() ,该四棱柱的上、下底面均为等腰梯形,分别内接于圆柱的上、下底面,下底面圆的圆心
,该四棱柱的上、下底面均为等腰梯形,分别内接于圆柱的上、下底面,下底面圆的圆心![]() 在梯形
在梯形![]() 内部,
内部,![]() ,
,![]() ,
,![]() ,设
,设![]() .
.
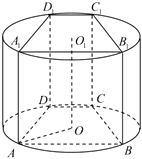
(1)求梯形![]() 的面积;
的面积;
(2)当![]() 取何值时,直四棱柱
取何值时,直四棱柱![]() 的体积最大?并求出最大值(注:木材的长度足够长)
的体积最大?并求出最大值(注:木材的长度足够长)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线C的参数方程为![]() (φ为参数),以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为
(φ为参数),以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为![]() .
.
(1)直线l与曲线C是否有公共点?并说明理由;
(2)若直线l与两坐标轴的交点为A,B,点P是曲线C上的一点,求△PAB的面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com