
 ,给出下列三个论断:
,给出下列三个论断: 对称;
对称; 对称.
对称. 可解得,∅=-
可解得,∅=- ,由此得f(x)=sin(2x-
,由此得f(x)=sin(2x- ),进行验证知f(x)的图象关于点
),进行验证知f(x)的图象关于点 对称,由此知
对称,由此知 .
. ,证明如下.
,证明如下. 对称
对称 +φ)=±1
+φ)=±1 +φ=2kπ±
+φ=2kπ± ,k∈Z
,k∈Z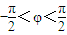 ,对k赋值知,∅=-
,对k赋值知,∅=-
 )
) )=0
)=0 =kπ,k∈Z
=kπ,k∈Z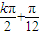 ,k∈Z,即对称中心的坐标是(
,k∈Z,即对称中心的坐标是( ,0)
,0) 对称.
对称.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
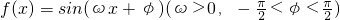 ,给出下列三个论断:
,给出下列三个论断: 对称;
对称;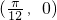 对称.
对称.查看答案和解析>>
科目:高中数学 来源: 题型:
设函数![]() ,给出下列三个论断:①
,给出下列三个论断:①![]() 的图象关于直线
的图象关于直线![]() 对称;②
对称;②![]() 的周期为
的周期为![]() ; ③
; ③![]() 的图象关于点
的图象关于点![]() 对称. 以其中的两个论断为条件,余下的一个论断作为结论,写出你认为正确的一个命题 。
对称. 以其中的两个论断为条件,余下的一个论断作为结论,写出你认为正确的一个命题 。
查看答案和解析>>
科目:高中数学 来源: 题型:
设函数![]() ,给出下列三个论断:①
,给出下列三个论断:①![]() 的图象关于直线
的图象关于直线![]() 对称;②
对称;②![]() 的周期为
的周期为![]() ; ③
; ③![]() 的图象关于点
的图象关于点![]() 对称. 以其中的两个论断为条件,余下的一个论断作为结论,写出你认为正确的一个命题 。
对称. 以其中的两个论断为条件,余下的一个论断作为结论,写出你认为正确的一个命题 。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com