
(本题12分)
设命题P:函数 在区间[-1,1]上单调递减;命题q:函数
在区间[-1,1]上单调递减;命题q:函数 的值域是R.如果命题p或q为真命题,p且q为假命题,求a的取值范围.
的值域是R.如果命题p或q为真命题,p且q为假命题,求a的取值范围.
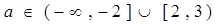 。
。
解析试题分析:p为真命题?f'(x)=3x2-a≤0在[-1,1]上恒成立?a≥3x2在[-1,1]上恒成立?a≥3
q为真命题?△=a2-4≥0恒成立?a≤-2或a≥2
由题意P和q有且只有一个是真命题p真q假?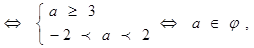
p假q真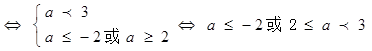 ?a≤-2或2≤a<3
?a≤-2或2≤a<3
综上所述:a∈(-∞,-2]∪[2,3)
考点:本试题主要考查了命题的真假判断和应用,解题时要注意合理地进行等价转化。
点评:解决该试题的关键由p为真命题,能够推导出a≥3.再由q为真命题,能够推导出a≤-2或a≥2.由题意P和q有且只有一个是真命题,所以p真q假? a≥3,-2< a <2,p假q真?a≤-2或2≤a<3.由此能够得到a的取值范围


科目:高中数学 来源: 题型:解答题
(1)已知命题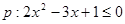 和命题
和命题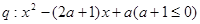 ,若
,若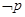 是
是 的必要不充分条件,求实数
的必要不充分条件,求实数 的取值范围.
的取值范围.
(2)已知命题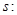 方程
方程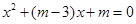 的一根在
的一根在 内,另一根在
内,另一根在 内.
内.
命题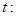 函数
函数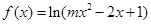 的定义域为全体实数.
的定义域为全体实数.
若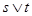 为真命题,求实数
为真命题,求实数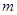 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
命题p: 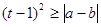 ,其中
,其中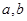 满足条件:五个数
满足条件:五个数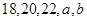 的平均数是20,标准差是
的平均数是20,标准差是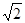 ; 命题q:m≤t≤n ,其中m,n满足条件:点M在椭圆
; 命题q:m≤t≤n ,其中m,n满足条件:点M在椭圆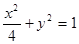 上,定点A(1,0),m、n分别为线段AM长的最小值和最大值。若命题“p或q”为真且命题“p且q”为假,求实数t的取值范围。
上,定点A(1,0),m、n分别为线段AM长的最小值和最大值。若命题“p或q”为真且命题“p且q”为假,求实数t的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分).设p:实数x满足 ,其中
,其中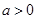 ,命题
,命题 实数
实数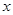 满足
满足 .
.
(I)若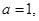 且
且 为真,求实数
为真,求实数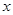 的取值范围;
的取值范围;
(II)若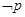 是
是
 的充分不必要条件,求实数a的取值范围.
的充分不必要条件,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com