
已知函数f(x),如果存在给定的实数对(a,b),使得f(a+x)·f(a-x)=b恒成立,则称f(x)为“S-函数”.
(Ⅰ)判断函数f1(x)=x,f2(x)=3x是否是“S-函数”;
(Ⅱ)若f3(x)=tanx是一个“S-函数”,求出所有满足条件的有序实数对(a,b);
(Ⅲ)若定义域为R的函数f(x)是“S-函数”,且存在满足条件的有序实数对(0,1)和(1,1),当x∈[0,1]时,f(x)的值域为[1,2],求当x∈[-2012,2012]时函数f(x)的值域.
|
解:(Ⅰ)若 即x2=a2-b时,对xÎ R恒成立.而x2=a2-b最多有两个解,矛盾. 因此 若 即存在常数对(a,32a)满足. 因此 (Ⅱ) 则tan(a-x)tan(a+x)=b恒成立. 当a= 因此 则有 即 即 当 因此满足 (Ⅲ)函数 于是 即 因此 当 |


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案科目:高中数学 来源: 题型:
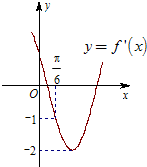 已知函数f(x)=sin(ωx+?)(ω>0,|?|<
已知函数f(x)=sin(ωx+?)(ω>0,|?|<| π | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
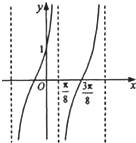 已知函数f(x)=Atan(ωx+φ)(ω>1,|φ|<
已知函数f(x)=Atan(ωx+φ)(ω>1,|φ|<| π |
| 2 |
| π |
| 24 |
A、2+
| ||||
B、
| ||||
C、
| ||||
D、2-
|
查看答案和解析>>
科目:高中数学 来源: 题型:
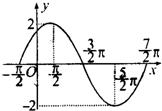 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<| π |
| 2 |
| 1 |
| 2 |
| 5 |
| 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2013•湛江一模)已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
(2013•湛江一模)已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<| π |
| 2 |
| π |
| 12 |
| 1 |
| 3 |
| π |
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com