
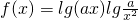
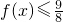 ,求a的范围.
,求a的范围.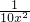
 =2×(-7)=-14
=2×(-7)=-14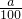 =(1+lga)(lga-2)=lg2a-lga-2=10
=(1+lga)(lga-2)=lg2a-lga-2=10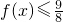

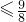 对一切正实数恒成立
对一切正实数恒成立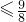
 对任意正实数x恒成立
对任意正实数x恒成立
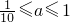 0
0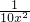 ,把x=1000代入可求
,把x=1000代入可求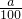 =(1+lga)(lga-2)=lg2a-lga-2=10可求lga,进而可求a
=(1+lga)(lga-2)=lg2a-lga-2=10可求lga,进而可求a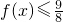 可得lg(ax)•lg
可得lg(ax)•lg
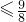 对一切正实数恒成立,整理可得
对一切正实数恒成立,整理可得 对任意正实数x恒成立,由x>0,lgx∈R,结合二次函数的性质可得,
对任意正实数x恒成立,由x>0,lgx∈R,结合二次函数的性质可得, ,从而可求
,从而可求

科目:高中数学 来源: 题型:
| a | 2x |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
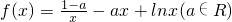
 处切线的斜率;
处切线的斜率;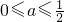 时,讨论f(x)的单调性;
时,讨论f(x)的单调性; 时,若对于任意x1∈(0,2),存在x2∈[1,2]使f(x1)≥g(x2)成立,求实数b的取值范围.
时,若对于任意x1∈(0,2),存在x2∈[1,2]使f(x1)≥g(x2)成立,求实数b的取值范围.查看答案和解析>>
科目:高中数学 来源:2012-2013学年江西省南昌市新建二中高二(上)12月月考数学试卷(理科)(解析版) 题型:解答题
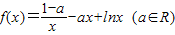
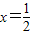 处切线的斜率;
处切线的斜率;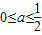 时,讨论f(x)的单调性;
时,讨论f(x)的单调性;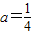 时,若对于任意x1∈(0,2),存在x2∈[1,2]使f(x1)≥g(x2)成立,求实数b的取值范围.
时,若对于任意x1∈(0,2),存在x2∈[1,2]使f(x1)≥g(x2)成立,求实数b的取值范围.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com