Question

【题目】已知椭圆C的中心在原点，焦点在x轴上，以两个焦点和短轴的两个端点为顶点的四边形是一个面积为8的正方形（记为Q）．

（Ⅰ）求椭圆C的方程；

（Ⅱ）设点P是直线x=﹣4与x轴的交点，过点P的直线l与椭圆C相交于M，N两点，当线段MN的中点落在正方形Q内（包括边界）时，求直线l斜率的取值范围．

Answer 1

【答案】

【解析】试题分析:（I）设出椭圆的方程，根据正方形的面积求出椭圆中参数a的值且判断出参数b，c的关系，根据椭圆的三个参数的关系求出b，c的值得到椭圆的方程．

（II）设出直线的方程，将直线的方程与椭圆方程联立，利用二次方程的韦达定理得到弦中点的坐标，根据中点在正方形的内部，得到中点的坐标满足的不等关系，求出k的范围．

解：（Ⅰ）依题意，设椭圆C的方程为，焦距为2c，

由题设条件知，a2=8，b=c

所以=4，

故椭圆的方程为；

（II）椭圆C的左准线方程为x=﹣4，所以点P的坐标为（﹣4，0）

显然直线l的斜率存在，所以设直线l的方程为y=k（x+4）

设点M，N的坐标分别为（x1，y1），（x2，y2），线段MN的中点为G（x0，y0）

由直线代入椭圆方程得（1+2k2）x2+16k2x+32k2﹣8=0．①

由△=（16k2）2﹣4（1+2k2）（32k2﹣8）＞0解得﹣＜k＜．②

因为x1，x2是方程①的两根，

所以x1+x2=﹣，于是x0==﹣，y0=．

因为x0==﹣≤0，所以点G不可能在y轴的右边，

又直线F1B2，F1B1方程分别为y=x+2，y=﹣x﹣2

所以点G在正方形Q内（包括边界）的充要条件为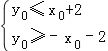，即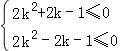

解得，此时②也成立．

故直线l斜率的取值范围是．