
如图所示,某旅游景点有一座风景秀丽的山峰,山上有一条笔直的山路BC和一条索道AC,小王和小李打算不坐索道,而是花2个小时的时间进行徒步攀登.已知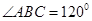 ,
,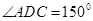 ,
,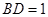 (千米),
(千米),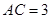 (千米).假设小王和小李徒步攀登的速度为每小时1200米,请问:两位登山爱好者能否在2个小时内徒步登上山峰.
(千米).假设小王和小李徒步攀登的速度为每小时1200米,请问:两位登山爱好者能否在2个小时内徒步登上山峰.
(即从B点出发到达C点)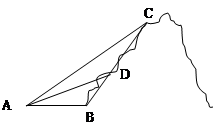
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:高中数学 来源: 题型:解答题
某人沿一条折线段组成的小路前进,从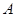 到
到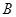 ,方位角(从正北方向顺时针转到
,方位角(从正北方向顺时针转到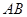 方向所成的角)是
方向所成的角)是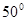 ,距离是3km;从
,距离是3km;从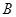 到
到 ,方位角是110°,距离是3km;从
,方位角是110°,距离是3km;从 到
到 ,方位角是140°,距离是(
,方位角是140°,距离是(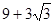 )km.试画出大致示意图,并计算出从A到D的方位角和距离(结果保留根号).
)km.试画出大致示意图,并计算出从A到D的方位角和距离(结果保留根号).
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
在直三棱柱ABC-A1B1C1中,已知AB=5,AC=4,BC=3,AA1=4,点D在棱AB上.
(1)若D是AB中点,求证:AC1∥平面B1CD;
(2)当 时,求二面角
时,求二面角 的余弦值.
的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com