
【题目】下列命题中,真命题是( )
A. 设![]() ,则
,则![]() 为实数的充要条件是
为实数的充要条件是![]() 为共轭复数;
为共轭复数;
B. “直线![]() 与曲线C相切”是“直线
与曲线C相切”是“直线![]() 与曲线C只有一个公共点”的充分不必要条件;
与曲线C只有一个公共点”的充分不必要条件;
C. “若两直线![]() ,则它们的斜率之积等于
,则它们的斜率之积等于![]() ”的逆命题;
”的逆命题;
D. ![]() 是R上的可导函数,“若
是R上的可导函数,“若![]() 是
是![]() 的极值点,则
的极值点,则![]() ”的否命题.
”的否命题.
【答案】C
【解析】
利用特殊值排除A选项.直线与预先相切,不一定只有一个公共点,排除B选项.写出C选项的逆命题,根据两直线垂直的条件判断C选项正确.写出D选项的否命题,根据极值点的概念,判断D选项不正确.
对于A选项,若![]() ,则
,则![]() 为实数,
为实数,![]() 不一定是共轭复数,故A选项错误.对于B选项. “直线
不一定是共轭复数,故A选项错误.对于B选项. “直线![]() 与曲线C相切”时,与曲线除了切点外,可能还有其它的公共点,故B选项错误.对于C选项,其逆命题为“若两条直线斜率的乘积为
与曲线C相切”时,与曲线除了切点外,可能还有其它的公共点,故B选项错误.对于C选项,其逆命题为“若两条直线斜率的乘积为![]() ,则
,则![]() ”,根据两条直线相互垂直的条件可知,这是真命题,C选项正确.对于D选项,原命题的否命题是“若
”,根据两条直线相互垂直的条件可知,这是真命题,C选项正确.对于D选项,原命题的否命题是“若![]() 不是
不是![]() 的极值点,则
的极值点,则![]() ”,这是错误的,如
”,这是错误的,如![]() ,
,![]() 时,
时,![]() ,而
,而![]() 不是
不是![]() 的极值点,因为导数为非负数,原函数在
的极值点,因为导数为非负数,原函数在![]() 上递增.所以原命题的否命题是假命题.综上所述,本题选C.
上递增.所以原命题的否命题是假命题.综上所述,本题选C.


科目:高中数学 来源: 题型:
【题目】某公司决定对旗下的某商品进行一次评估,该商品原来每件售价为25元,年销售8万件.
(1)据市场调查,若价格每提高1元,销售量将相应减少2000件,要使销售的总收入不低于原收入,该商品每件定价最多为多少元?
(2)为了抓住2022年冬奥会契机,扩大该商品的影响力,提高年销售量.公司决定立即对该商品进行全面技术革新和销售策略改革,并提高定价到![]() 元.公司拟投入
元.公司拟投入![]() 万作为技改费用,投入50万元作为固定宣传费用,投入
万作为技改费用,投入50万元作为固定宣传费用,投入![]() 万元作为浮动宣传费用.试问:当该商品改革后的销售量
万元作为浮动宣传费用.试问:当该商品改革后的销售量![]() 至少达到多少万件时,才可能使改革后的销售收入不低于原收入与总投入之和?并求出此时商品的每件定价.
至少达到多少万件时,才可能使改革后的销售收入不低于原收入与总投入之和?并求出此时商品的每件定价.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]()
![]() .若曲线
.若曲线![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() (
(![]() 为自然对数的底数).
为自然对数的底数).
(1)求函数![]() 的单调区间;
的单调区间;
(2)若关于![]() 的不等式
的不等式![]() 在(0,+
在(0,+![]() )上恒成立,求实数
)上恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】屠呦呦,第一位获得诺贝尔科学奖项的中国本土科学家,在2015年获得诺贝尔生理学或医学奖,理由是她发现了青蒿素.这种药品可以有效降低疟疾患者的死亡率,从青篙中提取的青篙素抗疟性超强,几乎达到100%.据监测:服药后每毫升血液中的含药量y(微克)与时间t(小时)之间近似满足如图所示的曲线.
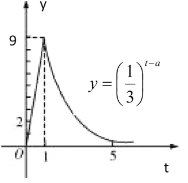
(Ⅰ)写出服药一次后y与t之间的函数关系式![]() ;
;
(Ⅱ)据进一步测定:每毫升血液中含药量不少于![]() 微克时,治疗有效,求服药一次后治疗有效的时间是多长?
微克时,治疗有效,求服药一次后治疗有效的时间是多长?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某重点中学将全部高一新生分成A,B两个成绩相当(成绩的均值、方差都相同)的级部,A级部采用传统形式的教学方式,B级部采用新型的基于信息化的自主学习教学方式.期末考试后分别从两个级部中各随机抽取100名学生的数学成绩进行统计,得到如下数据:
A级部教学 成绩分组 |
|
|
|
|
|
|
频数 | 18 | 23 | 29 | 23 | 6 | 1 |
B级部教学 成绩分组 |
|
|
|
|
|
|
频数 | 8 | 16 | 24 | 28 | 21 | 3 |
若成绩不低于130分者为“优秀”.
根据上表数据分别估计A,B两个级部“优秀”的概率;
(2)填写下面的列联表,并根据列联表判断是否有99%的把握认为“优秀”与教学方式有关?
是否优秀 级部 | 优秀 | 不优秀 | 合计 |
A级部 | |||
B级部 | |||
合计 |
(3)根据上表数据完成下面的频率分布直方图,并根据频率分布直方图,分别求出A,B两个级部的中位数的估计值(精确到![]() );请根据以上计算结果初步分析A,B两个级部的教学成绩的优劣.
);请根据以上计算结果初步分析A,B两个级部的教学成绩的优劣.

附表:
|
|
|
|
|
|
|
|
|
|
|
|
附: 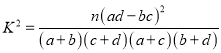
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (其中
(其中![]() ,
,![]() ),记函数
),记函数![]() 的导函数为
的导函数为![]() .
.
(Ⅰ)求函数![]() 的单调区间;
的单调区间;
(Ⅱ)是否存在实数![]() ,使得
,使得![]() 对任意正实数
对任意正实数![]() 恒成立?若存在,求出满足条件的实数
恒成立?若存在,求出满足条件的实数![]() ;若不存在,请说明理由.
;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系![]() 中,平行于
中,平行于![]() 轴且过点
轴且过点![]() 的入射光线
的入射光线![]() 被直线
被直线![]() 反射,反射光线
反射,反射光线![]() 交
交![]() 轴于
轴于![]() 点,圆
点,圆![]() 过点
过点![]() ,且与
,且与![]() 、
、![]() 相切.
相切.
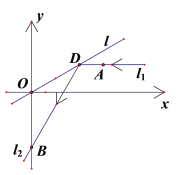
(Ⅰ)求![]() 所在直线的方程;
所在直线的方程;
(Ⅱ)求圆![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某射击运动员进行射击训练,前三次射击在靶上的着弹点![]() 刚好是边长为
刚好是边长为![]() 的等边三角形的三个顶点.
的等边三角形的三个顶点.

(Ⅰ)第四次射击时,该运动员瞄准![]() 区域射击(不会打到
区域射击(不会打到![]() 外),则此次射击的着弹点距
外),则此次射击的着弹点距![]() 的距离都超过
的距离都超过![]() 的概率为多少?(弹孔大小忽略不计)
的概率为多少?(弹孔大小忽略不计)
(Ⅱ) 该运动员前三次射击的成绩(环数)都在区间![]() 内,调整一下后,又连打三枪,其成绩(环数)都在区间
内,调整一下后,又连打三枪,其成绩(环数)都在区间![]() 内.现从这
内.现从这![]() 次射击成绩中随机抽取两次射击的成绩(记为
次射击成绩中随机抽取两次射击的成绩(记为![]() 和
和![]() )进行技术分析.求事件“
)进行技术分析.求事件“![]() ”的概率.
”的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com