
【题目】如图,已知正方形![]() 和矩形
和矩形![]() 所在的平面互相垂直,
所在的平面互相垂直,![]() ,
,![]() ,
,![]() 是线段
是线段![]() 的中点.
的中点.
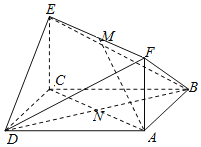
(1)求证![]() 平面
平面![]() ;
;
(2)求二面角![]() 的大小;
的大小;
(3)试在线段![]() 上一点
上一点![]() ,使得
,使得![]() 与
与![]() 所成的角是60°.
所成的角是60°.
【答案】(1)证明见解析;(2)60°;(3)点![]() 为线段
为线段![]() 的中点.
的中点.
【解析】
(1)根据正方形![]() 和矩形
和矩形![]() 所在的平面互相垂直,建立空间直角坐标系,求得
所在的平面互相垂直,建立空间直角坐标系,求得![]() 的坐标,证明共线即可.
的坐标,证明共线即可.
(2)根据![]() 平面
平面![]() ,得到
,得到![]() 为平面
为平面![]() 的一个法向量,由
的一个法向量,由![]() ,
,![]() ,得到
,得到![]() 为平面
为平面![]() 的一个法向量,然后代入公式
的一个法向量,然后代入公式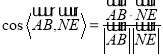 求解.
求解.
(3)设![]() ,求得
,求得![]() ,
,![]() 的坐标,代入公式
的坐标,代入公式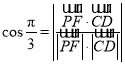 求解.
求解.
(1)建立如图所示的空间直角坐标系:
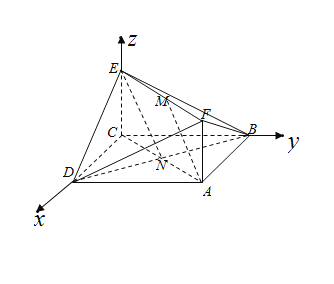
设![]() ,连接
,连接![]() ,
,
则点![]() 、
、![]() 的坐标分别是
的坐标分别是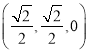 、
、![]() ,
,
∴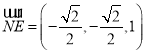 ,
,
又点![]() 、
、![]() 的坐标分别是
的坐标分别是![]() 、
、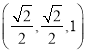 ,
,
∴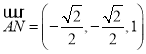 ,
,
∴![]() ,且
,且![]() 与
与![]() 不共线,
不共线,
∴![]() ,
,
又∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() .
.
(2)∵![]() ,
,![]() ,
,![]() ,
,
∴![]() 平面
平面![]() ,
,
∴![]() 为平面
为平面![]() 的一个法向量,
的一个法向量,
∵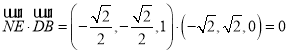 ,
,
∴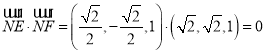 ,
,
得![]() ,
,![]() ,
,
∴![]() 为平面
为平面![]() 的一个法向量,
的一个法向量,
∴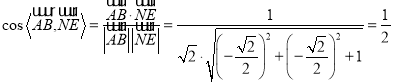 ,
,
∴![]() ,
,![]() 的夹角是60°,
的夹角是60°,
即所求二面角![]() 的大小是60°.
的大小是60°.
(3)设![]() ,
,![]() ,
,![]() ,
,
则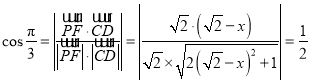 ,
,
解得![]() 或
或![]() (舍去),
(舍去),
所以当点![]() 为线段
为线段![]() 的中点时,直线
的中点时,直线![]() 与
与![]() 所成的角为60°.
所成的角为60°.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】用分期付款的方式购买某家用电器一件,价格为1 150元,购买当天先付150元,以后每月这一天还款一次,每次还款数额相同,20个月还清,月利率为1%,按复利计算.若交付150元后的第一个月开始算分期付款的第一个月,全部欠款付清后,请问买这件家电实际付款多少元?每月还款多少元?(最后结果保留4个有效数字)
参考数据:(1+1%)19=1.208,(1+1%)20=1.220,(1+1%)21=1.232.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年8月18日,举世瞩目的第18届亚运会在印尼首都雅加达举行,为了丰富亚运会志愿者的业余生活,同时鼓励更多的有志青年加入志愿者行列,大会主办方决定对150名志愿者组织一次有关体育运动的知识竞赛(满分120分)并计划对成绩前15名的志愿者进行奖励,现将所有志愿者的竞赛成绩制成频率分布直方图,如图所示,若第三组与第五组的频数之和是第二组的频数的3倍,试回答以下问题:
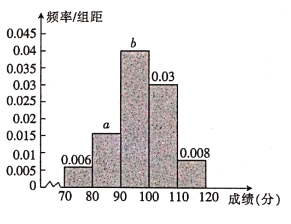
(1)求图中![]() 的值;
的值;
(2)求志愿者知识竞赛的平均成绩;
(3)从受奖励的15人中按成绩利用分层抽样抽取5人,再从抽取的5人中,随机抽取2人在主会场服务,求抽取的这2人中其中一人成绩在![]() 分的概率.
分的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】复旦大学附属华山医院感染科主任医师张文宏在接受媒体采访时谈到:通过救治研究发现,目前对于新冠肺炎最有用的“特效药”还是免疫力.而人的免疫力与体质息息相关,一般来讲,体质好,免疫力就强.复学已有一段时间,某医院到学校调查高二学生的体质健康情况,随机抽取12名高二学生进行体质健康测试,测试成绩(百分制)如下:65,78,90,86,52,87,72,86,87,98,88,86.根据此年龄段学生体质健康标准,成绩不低于80的为优良.
(1)将频率视为概率,根据样本估计总体的思想,在该学校全体高二学生中任选3人进行体质健康测试,求至少有1人成绩是“优良”的概率;
(2)从抽取的12人中随机选取3人,记![]() 表示成绩“优良”的人数,求
表示成绩“优良”的人数,求![]() 的分布列和期望.
的分布列和期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形ABCD为正方形,QA⊥平面ABCD,PD∥QA,QA=AB=![]() PD.
PD.
(1)证明:平面PQC⊥平面DCQ;
(2)求直线DQ与面PQC成角的正弦值
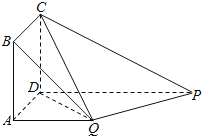
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() 的离心率为
的离心率为![]() ,右焦点
,右焦点![]() 到右准线的距离为3.(椭圆的右准线方程为
到右准线的距离为3.(椭圆的右准线方程为![]() )
)
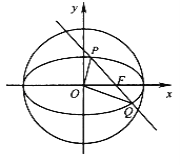
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设过![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点.已知
两点.已知![]() 被圆
被圆![]() 截得的弦长为
截得的弦长为![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知三棱锥![]() 的底面
的底面![]() 为正三角形,顶点在底面上的射影为底面的中心,
为正三角形,顶点在底面上的射影为底面的中心,![]() ,
,![]() 分别是棱
分别是棱![]() ,
,![]() 的中点,且
的中点,且![]() ,若侧棱
,若侧棱![]() ,则三棱锥
,则三棱锥![]() 的外接球的表面积是( )
的外接球的表面积是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将四个编号为1,2,3,4的相同小球放入编号为1,2,3,4的四个盒子中,
(1)若每个盒子放一个小球,求有多少种放法;
(2)若每个盒子放一球,求恰有1个盒子的号码与小球的号码相同的放法种数;
(3)求恰有一个空盒子的放法种数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com