
【题目】
某工厂有100名工人接受了生产1000台某产品的总任务,每台产品由9个甲型装置和3个乙型装置配套组成,每个工人每小时能加工完成1个甲型装置或3个乙型装置.现将工人分成两组分别加工甲型和乙型装置.设加工甲型装置的工人有x人,他们加工完甲型装置所需时间为t1小时,其余工人加工完乙型装置所需时间为t2小时.
设f(x)=t1+t2.
(Ⅰ)求f(x)的解析式,并写出其定义域;
(Ⅱ)当x等于多少时,f(x)取得最小值?
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知函数y=f(x)(x≠0)对于任意的x,y∈R且x,y≠0满足f(xy)=f(x)+f(y).
(1)求f(1),f(﹣1)的值;
(2)求证:y=f(x)为偶函数;
(3)若y=f(x)在(0,+∞)上是增函数,解不等式 ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在半径为3m的 ![]() 圆形(O为圆心)铝皮上截取一块矩形材料OABC,其中点B在圆弧上,点A、C在两半径上,现将此矩形铝皮OABC卷成一个以AB为母线的圆柱形罐子的侧面(不计剪裁和拼接损耗),设矩形的边长AB=xm,圆柱的体积为Vm3 .
圆形(O为圆心)铝皮上截取一块矩形材料OABC,其中点B在圆弧上,点A、C在两半径上,现将此矩形铝皮OABC卷成一个以AB为母线的圆柱形罐子的侧面(不计剪裁和拼接损耗),设矩形的边长AB=xm,圆柱的体积为Vm3 . 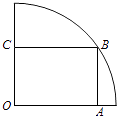
(1)写出体积V关于x的函数关系式,并指出定义域;
(2)当x为何值时,才能使做出的圆柱形罐子体积V最大?最大体积是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={x||x+1|<1},B={x|y= ![]() ,y∈R},则A∩RB=( )
,y∈R},则A∩RB=( )
A.(﹣2,1)
B.(﹣2,﹣1]
C.(﹣1,0)
D.[﹣1,0)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=kx,g(x)= ![]() .
.
(1)求函数g(x)= ![]() 的单调区间;
的单调区间;
(2)若不等式f(x)≥g(x)在区间(0,+∞)上恒成立,求实数k的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com