
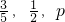 ,记1号小球放入甲盒为事件A,2号小球放入乙盒为事件B,3号小球放入丙盒为事件C,事件A、B、C相互独立.
,记1号小球放入甲盒为事件A,2号小球放入乙盒为事件B,3号小球放入丙盒为事件C,事件A、B、C相互独立.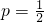 ,求事件A、B、C中至少有两件发生的概率;
,求事件A、B、C中至少有两件发生的概率; ,求p的取值范围.
,求p的取值范围.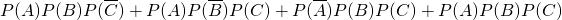
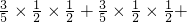
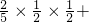
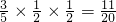 …(6分)
…(6分)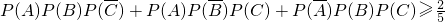 …(9分)
…(9分)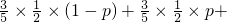
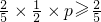
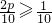
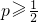 …(11分)
…(11分) …(12分)
…(12分)

 优生乐园系列答案
优生乐园系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| 3 |
| 5 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:2011-2012学年江西省高三第一次统考理科数学 题型:解答题
.将编号为1,2,3的三个小球随意放入编号为1,2,3的三个纸箱中,每个纸箱内有且只有一
个小球,称此为一轮“放球”,设一轮“放球”后编号为i(i=1,2,3)的纸箱放入的小球编号为ai,定义
吻合度误差为 =|1-a1|+|2-a2|+|3-a3|。假设a1,a2,a3等可能地为1、2、3的各种排列,求⑴某人一
=|1-a1|+|2-a2|+|3-a3|。假设a1,a2,a3等可能地为1、2、3的各种排列,求⑴某人一
轮“放球”满足 =2时的概率。⑵
=2时的概率。⑵ 的数学期望。
的数学期望。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com