C
分析:先求出f(x)在区间(-1,2]上的解析式,令g(x)=f(x)-mx-m=0,即有f(x)=mx+m,在同一坐标系内画出y=f(x)和y=mx+m的图象,
转化为图象有三个不同的交点的条件,数形结合求出实数m的取值范围.
解答:

解:当x∈(-1,0]时,x+1∈(0,1],f(x)=x,由函数f(x)满足f(x+1)[f(x)+1]=1可得,
f(x)=
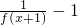
=
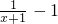
=-

.
当x∈[1,2]时,x-1∈[0,1],由f(x+1)[f(x)+1]=1可得 f(x)[f(x-1)+1]=1,故 f(x)=

=

.
由g(x)=f(x)-m(x+1)在区间(-1,2]有3个零点,可得函数 y=f(x)的图象和y=mx+m的图象有3个交点.
在同一坐标系内画出y=f(x)和y=mx+m的图象,如图所示:
动直线y=mx+m过定点(-1,0),当x=1时,y=2m<1,当x=2时,y=3m≥

,解得

≤m<

.
由图象可知当

≤m<

时,两图象有三个不同的交点,从而g(x)=f(x)-mx-m有三个不同的零点,
故选C.
点评:本题考查函数零点的意义及个数求解.函数与方程的思想.利用函数的图象可以加强直观性,本题先由已知条件转化为判断两函数图象交点个数,再利用函数图象解决.

 )
) )
)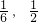 )
) )
) 解:当x∈(-1,0]时,x+1∈(0,1],f(x)=x,由函数f(x)满足f(x+1)[f(x)+1]=1可得,
解:当x∈(-1,0]时,x+1∈(0,1],f(x)=x,由函数f(x)满足f(x+1)[f(x)+1]=1可得,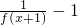 =
=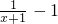 =-
=- .
. =
= .
. ,解得
,解得  ≤m<
≤m< .
. ≤m<
≤m< 时,两图象有三个不同的交点,从而g(x)=f(x)-mx-m有三个不同的零点,
时,两图象有三个不同的交点,从而g(x)=f(x)-mx-m有三个不同的零点,
