已知函数f(x)＝2sin
cos＋
cos
.
（1）求函数f(x)的最小正周期及最值；
（2）令g(x)＝f
，判断函数g(x)的奇偶性，并说明理由．
（1） 最小正周期4
;（2） 函数g（x）是偶函数．
解析试题分析：（1）利用两角和的正弦函数化简函数为一个角的一个三角函数的形式，然后直接求f（x）的最小正周期；（2）求出g(x)＝f的表达式，通过函数的奇偶性的定义，直接证明即可．
试题解析：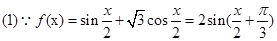
2分
∴f（x）的最小正周期T=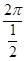
=4 .1分
当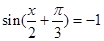
时，f（x）取得最小值-2； 1分
当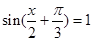
时，f（x）取得最大值2 .1分
（2）g（x）是偶函数．理由如下： .1分
由（1）知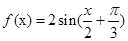
,又g（x）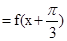
∴g（x）=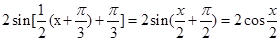 
3..分
∵g（-x）=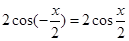
=g（x）， .2分
∴函数g（x）是偶函数 ..1分
考点：三角函数中的恒等变换应用；三角函数的周期性及其求法；正弦函数的奇偶性.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
，α为第三象限角．
，
的值；
），tan2α的值．
.
；
是第三象限角，且
，求
，
，且
.求：
的值；（2）
的值.
，
. 
；
中，内角
所对边长分别为
，
，
．
的最大值及
的取值范围；
的值域．
的最小正周期;
的值．
的单调增区间
，其中
时，求
在区间
上的最大值与最小值；
，求
的值.
时，求函数
取得最大值和最小值时
的值；
的内角A、B、C的对应边分别是
，且
，若向量
与向量
平行，求
的值.