
【题目】已知函数![]()
(1)求函数f(x)是单调区间;
(2)如果关于x的方程![]() 有实数根,求实数
有实数根,求实数![]() 的取值集合;
的取值集合;
(3)是否存在正数k,使得关于x的方程![]() 有两个不相等的实数根?如果存在,求k满足的条件;如果不存在,说明理由.
有两个不相等的实数根?如果存在,求k满足的条件;如果不存在,说明理由.
【答案】(1) ![]() 是函数的增区间;(-1,0)和(0,3)是函数的减区间;
是函数的增区间;(-1,0)和(0,3)是函数的减区间;
(2) 实数m的取值范围是![]() ;(3) 满足条件的正数k不存在.
;(3) 满足条件的正数k不存在.
【解析】试题分析:(1)先求函数导数,再求导函数零点,列表分析导函数符号变化规律,确定单调区间,(2)分离参变得求函数![]() 值域,利用导数求
值域,利用导数求![]() 值域,(3)由于
值域,(3)由于![]() 为
为![]() 恒正递增函数,
恒正递增函数, ![]() 是
是![]() 上恒正减函数,因此可得矛盾,即推得不存在
上恒正减函数,因此可得矛盾,即推得不存在
试题解析:(1)函数![]() 的定义域是
的定义域是![]()
对![]() 求导得
求导得 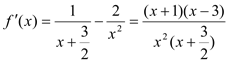
由 ![]() ,由
,由![]()
因此 ![]() 是函数
是函数![]() 的增区间;
的增区间;
(-1,0)和(0,3)是函数![]() 的减区间
的减区间
(2)因为![]()
所以实数m的取值范围就是函数![]() 的值域
的值域
对![]()
令![]()
∴当x=2时![]() 取得最大值,且
取得最大值,且![]()
又当x无限趋近于0时,![]() 无限趋近于
无限趋近于![]() 无限趋近于0,
无限趋近于0,
进而有![]() 无限趋近于-∞.因此函数
无限趋近于-∞.因此函数![]() 的值域是
的值域是 ![]()
即实数m的取值范围是![]()
(3)结论:这样的正数k不存在。
证明:假设存在正数k,使得关于x的方程
![]() 有
有![]() 两个不相等的实数根
两个不相等的实数根![]() ,则
,则
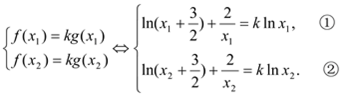
根据对数函数定义域知![]() 都是正数。
都是正数。
又由(1)可知,当 ![]()
∴![]() =
=![]()
再由k>0,可得![]()
由于 ![]() 不妨设
不妨设 ![]() ,由①和②可得
,由①和②可得 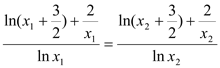
利用比例性质得 
即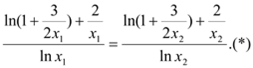
由于![]() 上的恒正增函数,且
上的恒正增函数,且 ![]()
又由于 ![]() 上的恒正减函数,且
上的恒正减函数,且 ![]() ∴
∴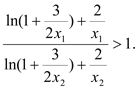
∴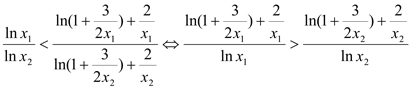 ,这与(*)式矛盾。因此满足条件的正数k不存在.
,这与(*)式矛盾。因此满足条件的正数k不存在.


 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)若函数![]() 在
在![]() 上是减函数,求实数
上是减函数,求实数![]() 的取值范围;
的取值范围;
(2)当![]() 时,分别求函数
时,分别求函数![]() 的最小值和
的最小值和![]() 的最大值,并证明当
的最大值,并证明当![]() 时,
时, ![]() 成立;
成立;
(3)令![]() ,当
,当![]() 时,判断函数
时,判断函数![]() 有几个不同的零点并证明.
有几个不同的零点并证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4—4:坐标系与参数方程选讲.
在平面直角坐标系![]() 中,以
中,以![]() 为极点,
为极点,![]() 轴的正半轴为极轴的极坐标系中,直线
轴的正半轴为极轴的极坐标系中,直线![]() 的极坐标方程为
的极坐标方程为![]() ,曲线
,曲线![]() 的参数方程为
的参数方程为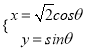 .
.
(1)写出直线![]() 与曲线
与曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)过点M平行于直线![]() 的直线与曲线
的直线与曲线![]() 交于
交于![]() 两点,若
两点,若![]() ,求点M轨迹的直角坐标方程.
,求点M轨迹的直角坐标方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
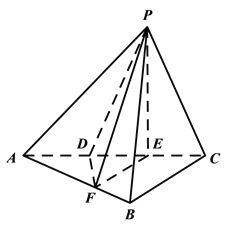
【题目】如图,三棱锥P-ABC中,平面PAC![]() 平面ABC,
平面ABC, ![]() ABC=
ABC=![]() ,点D、E在线段AC上,且AD=DE=EC=2,PD=PC=4,点F在线段AB上,且EF//BC.
,点D、E在线段AC上,且AD=DE=EC=2,PD=PC=4,点F在线段AB上,且EF//BC.
(Ⅰ)证明:AB![]() 平面PFE.
平面PFE.
(Ⅱ)若四棱锥P-DFBC的体积为7,求线段BC的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某项运动组委会为了搞好接待工作,招募了16名男志愿者和14名女志愿者,调查发现,男、女志愿者中分别有10人和6人喜爱运动,其余人不喜爱运动.得到下表:
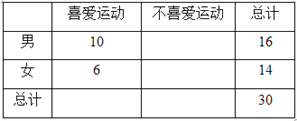
(1)根据以上数据完成2×2列联表, 问:能否在犯错误的概率不超过0.10的前提下,认为性别与喜爱运动有关?并说明理由.
(2)如果从喜欢运动的女志愿者中(其中恰有4人会外语)抽取2名,求抽出的志愿者中能胜任翻译工作的人数![]() 的分布列及数学期望.
的分布列及数学期望.
参考公式: 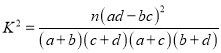
参考数据:

查看答案和解析>>
科目:高中数学 来源: 题型:
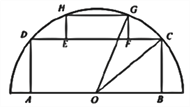
【题目】如图,有一块半圆形空地,开发商计划建一个矩形游泳池![]() 及其矩形附属设施
及其矩形附属设施![]() ,并将剩余空地进行绿化,园林局要求绿化面积应最大化.其中半圆的圆心为
,并将剩余空地进行绿化,园林局要求绿化面积应最大化.其中半圆的圆心为![]() ,半径为
,半径为![]() ,矩形的一边
,矩形的一边![]() 在直径上,点
在直径上,点![]() 在圆周上,
在圆周上, ![]() 在边
在边![]() 上,且
上,且![]() ,设
,设![]() .
.
(1)记游泳池及其附属设施的占地面积为![]() ,求
,求![]() 的表达式;
的表达式;
(2)当![]() 为何值时,能符合园林局的要求?
为何值时,能符合园林局的要求?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com