
| 日期 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| AQI | 89 | 55 | 52 | 87 | 124 | 72 | 65 | 26 | 46 | 48 |
| 日期 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| AQI | 58 | 36 | 63 | 78 | 89 | 97 | 74 | 78 | 90 | 117 |
| 日期 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
| AQI | 137 | 139 | 77 | 63 | 63 | 77 | 64 | 65 | 55 | 45 |
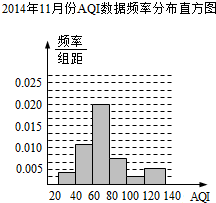
| 分组 | 频数 | 频率 |
| [20,40) | ||
| [40,60) | ||
| [60,80) | ||
| [80,100) | ||
| [100,120) | ||
| [120,140] |

| 分组 | 频数 | 频率 | ||
| [20,40) | 2 |
| ||
| [40,60) | 7 |
| ||
| [60,80) | 12 |
| ||
| [80,100) | 5 |
| ||
| [100,120) | 1 |
| ||
| [120,140] | 3 |
|
| 1 |
| 3 |
| 19 |
| 30 |
| 26 |
| 30 |
| 26 |
| 30 |
| 19 |
| 30 |
| 7 |
| 30 |


 学习实践园地系列答案
学习实践园地系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| 车站 | 怀集站 | 广宁站 | 肇庆东站 | 三水南站 | 佛山西站 | 广州南站 |
| 满意度得分 | 70 | 76 | 72 | 70 | 72 | x |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com