
【题目】已知若![]() ,则称
,则称![]() 为
为![]() 的原函数,此时
的原函数,此时![]() 所有的原函数为
所有的原函数为![]() ,其中
,其中![]() 为常数,如:
为常数,如:![]() ,则
,则![]() (
(![]() 为常数).现已知函数
为常数).现已知函数![]() 的导函数为
的导函数为![]() 且对任意的实数
且对任意的实数![]() 都有
都有![]() (
(![]() 是自然对数的底数),且
是自然对数的底数),且![]() ,若关于
,若关于![]() 的不等式
的不等式![]() 的解集中恰有两个整数,则实数
的解集中恰有两个整数,则实数![]() 的取值范围是( )
的取值范围是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】[选修4—4:坐标系与参数方程]
在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数,![]() ),以坐标原点
),以坐标原点![]() 为极点,
为极点,![]() 轴的非负半轴为极轴,建立极坐标系,直线
轴的非负半轴为极轴,建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)设![]() 是曲线
是曲线![]() 上的一个动眯,当
上的一个动眯,当![]() 时,求点
时,求点![]() 到直线
到直线![]() 的距离的最小值;
的距离的最小值;
(2)若曲线![]() 上所有的点都在直线
上所有的点都在直线![]() 的右下方,求实数
的右下方,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在![]() 中,已知
中,已知![]() ,
,![]() ,D是边AC上的一点,将
,D是边AC上的一点,将![]() 沿BD折叠,得到三棱锥
沿BD折叠,得到三棱锥![]() ,若该三棱锥的顶点A在底面BCD的射影M在线段BC上,设
,若该三棱锥的顶点A在底面BCD的射影M在线段BC上,设![]() ,则x的取值范围是( )
,则x的取值范围是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某隧道的剖面图是由半圆及矩形![]() 组成,交通部门拟在隧道顶部安装通风设备(视作点
组成,交通部门拟在隧道顶部安装通风设备(视作点![]() ),为了固定该设备,计划除从隧道最高点
),为了固定该设备,计划除从隧道最高点![]() 处使用钢管垂直向下吊装以外,再在两侧自
处使用钢管垂直向下吊装以外,再在两侧自![]() 两点分别使用钢管支撑.已知道路宽
两点分别使用钢管支撑.已知道路宽![]() ,设备要求安装在半圆内部,所使用的钢管总长度为
,设备要求安装在半圆内部,所使用的钢管总长度为![]() .
.
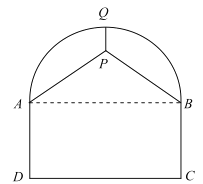
(1)①设![]() ,将
,将![]() 表示为关于
表示为关于![]() 的函数;
的函数;
②设![]() ,将
,将![]() 表示为关于
表示为关于![]() 的函数;
的函数;
(2)请选用(1)中的一个函数关系式,说明如何设计,所用的钢管材料最省?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,椭圆
中,椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,
,![]() 为
为![]() 椭圆上一点,且
椭圆上一点,且![]() 垂直于
垂直于![]() 轴,连结
轴,连结![]() 并延长交椭圆于另一点
并延长交椭圆于另一点![]() ,设
,设![]() .
.

(1)若点![]() 的坐标为
的坐标为![]() ,求椭圆
,求椭圆![]() 的方程及
的方程及![]() 的值;
的值;
(2)若![]() ,求椭圆
,求椭圆![]() 的离心率的取值范围.
的离心率的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若在两个成语中,一个成语的末字恰是另一成语的首字,则称这两个成语有顶真关系,现从分别贴有成语“人定胜天”、“争先恐后”、“一马当先”、“天马行空”、“先发制人”的5张大小形状完全相同卡片中,任意抽取2张,则这2张卡片上的成语有顶真关系的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班随机抽查了![]() 名学生的数学成绩,分数制成如图的茎叶图,其中
名学生的数学成绩,分数制成如图的茎叶图,其中![]() 组学生每天学习数学时间不足
组学生每天学习数学时间不足![]() 个小时,
个小时,![]() 组学生每天学习数学时间达到一个小时,学校规定
组学生每天学习数学时间达到一个小时,学校规定![]() 分及
分及![]() 分以上记为优秀,
分以上记为优秀,![]() 分及
分及![]() 分以上记为达标,
分以上记为达标,![]() 分以下记为未达标.
分以下记为未达标.

(1)根据茎叶图完成下面的列联表:
达标 | 未达标 | 总计 | |
| |||
| |||
总计 |
(2)判断是否有![]() 的把握认为“数学成绩达标与否”与“每天学习数学时间能否达到一小时”有关.
的把握认为“数学成绩达标与否”与“每天学习数学时间能否达到一小时”有关.
参考公式与临界值表: ,其中
,其中![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com