
【题目】某商场为吸引顾客消费推出一项优惠活动.活动规则如下:消费额每满100元可转动如图所示的转盘一次,并获得相应金额的返券,假定指针等可能地停在任一位置.若指针停在A区域返券60元;停在B区域返券30元;停在C区域不返券.例如:消费218元,可转动转盘2次,所获得的返券金额是两次金额之和.

(1)若某位顾客消费128元,求返券金额不低于30元的概率;
(2)若某位顾客恰好消费280元,并按规则参与了活动,他获得返券的金额记为![]() (元).求随机变量
(元).求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
【答案】(1)![]() ;(2)随机变量
;(2)随机变量![]() 的分布列为:
的分布列为:
| 0 | 30 | 60 | 90 | 120 |
|
|
|
|
|
|
其数学期望![]() .
.
【解析】试题分析:(1)由题意可知,A区扇形区域的圆心角为![]() ,根据几何概型可知,指针停在A区的概率为
,根据几何概型可知,指针停在A区的概率为![]() ,同理可求指针落在B区域的概率为
,同理可求指针落在B区域的概率为![]() ,指针落在C区域的概率为
,指针落在C区域的概率为![]() ,所以若某位顾客消费128元,根据规则,可以转动一次转盘,若返券金额不低于30元,则指针落在A区域或落在B区域,而由于指针落在A区域或落在B区域为互斥事件,根据互斥事件概率加法公式,返券金额不低于30元的概率为
,所以若某位顾客消费128元,根据规则,可以转动一次转盘,若返券金额不低于30元,则指针落在A区域或落在B区域,而由于指针落在A区域或落在B区域为互斥事件,根据互斥事件概率加法公式,返券金额不低于30元的概率为![]() ;
;
(2)若某位顾客消费280,则可以转动2次转盘,那么他获得返券的金额X的所有可能取值为0,30,60,90,120,概率为![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 。即得到X的分布列,然后可以根据公式求X的数学期望。
。即得到X的分布列,然后可以根据公式求X的数学期望。
试题解析:设指针落在A,B,C区域分别记为事件A,B,C. 则
![]() .
.
(1)若返券金额不低于30元,则指针落在A或B区域.即
![]()
所以消费128元的顾客,返券金额不低于30元的概率是![]() .
.
(2)由题意得,该顾客可转动转盘2次,随机变量![]() 的可能值为0,30,60,90,120
的可能值为0,30,60,90,120
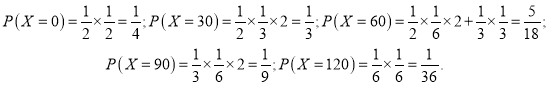
所以,随机变量![]() 的分布列为:
的分布列为:
| 0 | 30 | 60 | 90 | 120 |
|
|
|
|
|
|
其数学期望![]()


科目:高中数学 来源: 题型:
【题目】如图,圆![]() :
: ![]() .
.
(1)若圆![]() 与
与![]() 轴相切,求圆
轴相切,求圆![]() 的方程;
的方程;
(2)求圆心![]() 的轨迹方程;
的轨迹方程;
(3)已知![]() ,圆
,圆![]() 与
与![]() 轴相交于两点
轴相交于两点![]() (点
(点![]() 在点
在点![]() 的左侧).过点
的左侧).过点![]() 任作一条直线与圆
任作一条直线与圆![]() :
: ![]() 相交于两点
相交于两点![]() .问:是否存在实数
.问:是否存在实数![]() ,使得
,使得![]() ?若存在,求出实数
?若存在,求出实数![]() 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]()
![]() 的左、右顶点分别为
的左、右顶点分别为![]() 、
、![]() ,上、下顶点分别为
,上、下顶点分别为![]() 、
、![]() ,
, ![]() 为坐标原点,四边形
为坐标原点,四边形![]() 的面积为
的面积为![]() ,且该四边形内切圆的方程为
,且该四边形内切圆的方程为![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)若![]() 、
、![]() 是椭圆
是椭圆![]() 上的两个不同的动点,直线
上的两个不同的动点,直线![]() 、
、![]() 的斜率之积等于
的斜率之积等于![]() ,试探求
,试探求![]() 的面积是否为定值,并说明理由.
的面积是否为定值,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和Sn=3n+m(m为常数,n∈N+)
(1)求a1 , a2 , a3;
(2)若数列{an}为等比数列,求常数m的值及an;
(3)对于(2)中的an , 记f(n)=λa2n+1﹣4λan+1﹣7,若f(n)<0对任意的正整数n恒成立,求实数λ的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一次爱心捐款活动中,小李为了了解捐款数额是否和居民自身的经济收入有关,随机调査了某地区的![]() 个捐款居民每月平均的经济收入. 在捐款超过
个捐款居民每月平均的经济收入. 在捐款超过![]() 元的居民中,每月平均的经济收入没有达到
元的居民中,每月平均的经济收入没有达到![]() 元的有
元的有![]() 个,达到
个,达到![]() 元的有
元的有![]() 个;在捐款不超过
个;在捐款不超过![]() 元的居民中,每月平均的经济收入没有达到
元的居民中,每月平均的经济收入没有达到![]() 元的有
元的有![]() 个.
个.
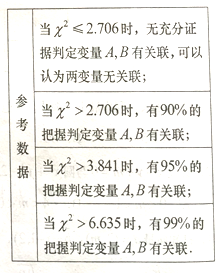
(1)在下图表格空白处填写正确数字,并说明是否有![]() 以上的把握认为捐款数额是否超过
以上的把握认为捐款数额是否超过![]() 元和居民毎月平均的经济收入是否达到
元和居民毎月平均的经济收入是否达到![]() 元有关?
元有关?
(2)将上述调查所得到的频率视为概率. 现在从该地区大量居民中,采用随机抽样方法毎次抽取![]() 个居民,共抽取
个居民,共抽取![]() 次,记被抽取的
次,记被抽取的![]() 个居民中经济收入达到
个居民中经济收入达到![]() 元的人数为
元的人数为![]() ,求
,求![]() 和期望
和期望![]() 的值.
的值.
每月平均经济收入达到 | 每月平均经济收入没有达到 | 合计 | |
捐款超过 | |||
捐款不超过 | |||
合计 |
附: 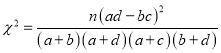 ,其中
,其中![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆心在![]() 轴上的圆
轴上的圆![]() 与直线
与直线![]() 切于点
切于点![]() .
.
(1)求圆![]() 的标准方程;
的标准方程;
(2)已知![]() ,经过原点,且斜率为正数的直线
,经过原点,且斜率为正数的直线![]() 与圆
与圆![]() 交于
交于![]() 两点.
两点.
(ⅰ)求证: ![]() 为定值;
为定值;
(ⅱ)求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学数学老师分别用两种不同教学方式对入学数学平均分和优秀率都相同的甲、乙两个高一新班(人数均为20人)进行教学(两班的学生学习数学勤奋程度和自觉性一致),数学期终考试成绩茎叶图如下:
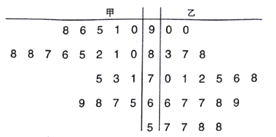
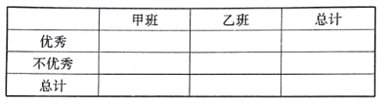
(1)学校规定:成绩不低于75分的为优秀,请填写下面的![]() 联表,并判断有多大把握认为“成绩优秀与教学方式有关”.
联表,并判断有多大把握认为“成绩优秀与教学方式有关”.
附:参考公式及数据

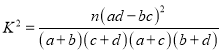
(2)从两个班数学成绩不低于90分的同学中随机抽取3名,设![]() 为抽取成绩不低于95分同学人数,求
为抽取成绩不低于95分同学人数,求![]() 的分布列和期望.
的分布列和期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com