
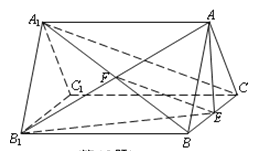
【题目】在直三棱柱ABC-A1B1C1中,AB=AC,E是BC的中点,求证:
(Ⅰ)平面AB1E⊥平面B1BCC1;
(Ⅱ)A1C//平面AB1E.

【答案】(1)见解析(2)见解析
【解析】试题分析:(1)先根据直棱柱的性质,可得![]() 平面
平面![]() ,可得
,可得![]() ,再根据等腰三角形性质可得
,再根据等腰三角形性质可得![]() ,从而可得
,从而可得![]() 平面
平面![]() ,进而得出结果;(2)连接
,进而得出结果;(2)连接![]() ,设
,设![]() ,连接
,连接![]() ,由平行四边形的性质结合中位线定理可得
,由平行四边形的性质结合中位线定理可得![]() .根据线面平行的判定定理可得结果.
.根据线面平行的判定定理可得结果.
试题解析:(1)在直三棱柱ABC-A1B1C1中,CC1平面ABC.
因为AE![]() 平面ABC,
平面ABC,
所以CC1![]() AE.
AE.
因为AB=AC,E为BC的中点,所以AE![]() BC.
BC.
因为BC在平面B1BCC1,内,CC1在平面B1BCC1内
且BC∩CC1=C,
所以AE![]() 平面B1BCC1.
平面B1BCC1.
因为AE在平面AB1E内
所以平面AB1E![]() 平面B1BCC1.
平面B1BCC1.
(2)连接A1B,设A1B∩AB1=F,连接EF.
在直三棱柱ABC-A1B1C1中,四边形AA1B1B为平行四边形,
所以F为A1B的中点.
又因为E是BC的中点,所以EF∥A1C.
因为EF在平面AB1E内,A1C不在平面AB1E内,
所以A1C∥平面AB1E.
【方法点晴】本题主要考查线面平行的判定定理以及线面垂直、面面垂直的判定,属于难题.证明线面平行的常用方法:①利用线面平行的判定定理,使用这个定理的关键是设法在平面内找到一条与已知直线平行的直线,可利用几何体的特征,合理利用中位线定理、线面平行的性质或者构造平行四边形、寻找比例式证明两直线平行.②利用面面平行的性质,即两平面平行,在其中一平面内的直线平行于另一平面. 本题(2)是就是利用方法①证明的.


科目:高中数学 来源: 题型:
【题目】已知定义域为R的函数f(x)= ![]() 是奇函数.
是奇函数.
(Ⅰ)求a,b的值;
(Ⅱ)若对任意的t∈R,不等式f(t2﹣2t)+f(2t2﹣k)<0恒成立,求k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=( ![]() )x , g(x)=x2 , 对于不相等的实数x1 , x2 , 设m=
)x , g(x)=x2 , 对于不相等的实数x1 , x2 , 设m= ![]() ,n=
,n= ![]() ,则下列说法正确的有( )
,则下列说法正确的有( )
①对于任意不相等的实数x1 , x2 , 都有m<0;
②对于任意不相等的实数x1 , x2 , 都有n<0;
③存在不相等的实数x1 , x2 , 使得m=n.
A.①
B.①③
C.②③
D.①②③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
已知数列{an}的各项均为正数,记数列{an}的前n项和为Sn,数列{an2}的前n项和为Tn,且3Tn=Sn2+2Sn,n∈N*.
(Ⅰ)求a1的值;
(Ⅱ)求数列{an}的通项公式;
(Ⅲ)若k,t∈N*,且S1,Sk-S1,St-Sk成等比数列,求k和t的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】继共享单车之后,又一种新型的出行方式------“共享汽车”也开始亮相北上广深等十余大中城市,一款叫“一度用车”的共享汽车在广州提供的车型是“奇瑞eQ”,每次租车收费按行驶里程加用车时间,标准是“1元/公里+0.1元/分钟”,李先生家离上班地点10公里,每天租用共享汽车上下班,由于堵车因素,每次路上开车花费的时间是一个随机变量,根据一段时间统计40次路上开车花费时间在各时间段内的情况如下:
时间(分钟) |
|
|
|
|
|
次数 | 8 | 14 | 8 | 8 | 2 |
以各时间段发生的频率视为概率,假设每次路上开车花费的时间视为用车时间,范围为![]() 分钟.
分钟.
(Ⅰ)若李先生上.下班时租用一次共享汽车路上开车不超过45分钟,便是所有可选择的交通工具中的一次最优选择,设![]() 是4次使用共享汽车中最优选择的次数,求
是4次使用共享汽车中最优选择的次数,求![]() 的分布列和期望.
的分布列和期望.
(Ⅱ)若李先生每天上下班使用共享汽车2次,一个月(以20天计算)平均用车费用大约是多少(同一时段,用该区间的中点值作代表).
查看答案和解析>>
科目:高中数学 来源: 题型:
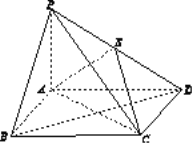
【题目】(本题满分12分)如图13,四棱锥P ABCD中,底面ABCD为矩形,PA⊥平面ABCD,E为PD的中点.
(1)证明:PB∥平面AEC;
(2)设AP=1,AD=![]() ,三棱锥P ABD的体积V=
,三棱锥P ABD的体积V=![]() ,求A到平面PBC的距离.
,求A到平面PBC的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)= ![]() x3+ax2﹣8x﹣1(a<0).若曲线y=f(x)的切线斜率的最小值是﹣9.求:
x3+ax2﹣8x﹣1(a<0).若曲线y=f(x)的切线斜率的最小值是﹣9.求:
(1)a的值;
(2)函数f(x)的极值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)对任意的x,y∈R,总有f(x)+f(y)=f(x+y),且x<0时,f(x)>0.
(1)求证:函f(x)是奇函数;
(2)求证:函数f(x)是R上的减函数;
(3)若定义在(﹣2,2)上的函数f(x)满足f(﹣m)+f(1﹣m)<0,求实数m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com