
【题目】已知命题p:x∈[-1,2],函数f(x)=x2-x的值大于0,若p∨q是真命题,则命题q可以是( )
A. x0∈(-1,1),cos x0<![]()
B. “-3<m<0”是“函数f(x)=x+log2x+m在区间![]() 上有零点”的必要不充分条件
上有零点”的必要不充分条件
C. x=![]() 是曲线f(x)=
是曲线f(x)=![]() sin 2x+cos 2x的一条对称轴
sin 2x+cos 2x的一条对称轴
D. 若x∈(0,2),则在曲线f(x)=ex(x-2)上任意一点处的切线的斜率不小于![]()
【答案】C
【解析】
由题意易知p是假命题,故只需q是真命题,逐一判断选项即可解决.
对于命题p:函数f(x)=x2-x=![]() ,则函数f(x)在
,则函数f(x)在![]() 上单调递减,在
上单调递减,在![]() 上单调递增.∴当x=
上单调递增.∴当x=![]() 时,f(x)取得最小值,
时,f(x)取得最小值,![]() ,因此命题p是假命题.若p∨q是真命题,则命题q必须是真命题.A中,x∈(-1,1),cos x∈(cos 1,1],而cos 1>
,因此命题p是假命题.若p∨q是真命题,则命题q必须是真命题.A中,x∈(-1,1),cos x∈(cos 1,1],而cos 1>![]() ,因此A是假命题;B中,函数f(x)=x+log2x+m在区间
,因此A是假命题;B中,函数f(x)=x+log2x+m在区间![]() 上单调递增,若函数f(x)在此区间上有零点,则
上单调递增,若函数f(x)在此区间上有零点,则![]() ,解得
,解得![]() ,因此“-3<m<0”是“函数f(x)=x+log2x+m在区间
,因此“-3<m<0”是“函数f(x)=x+log2x+m在区间![]() 上有零点”的充分不必要条件,因此B是假命题;C中,f(x)=
上有零点”的充分不必要条件,因此B是假命题;C中,f(x)=![]() sin 2x+cos 2x=
sin 2x+cos 2x=![]() ,当x=
,当x=![]() 时,
时,![]() ,因此x=
,因此x=![]() 是曲线y=f(x)的一条对称轴,C是真命题;D中,f(x)=ex(x-2),f′(x)=ex+ex(x-2)=ex(x-1),当x∈(0,2)时,f′(x)>f′(0)=-1,因此D是假命题.
是曲线y=f(x)的一条对称轴,C是真命题;D中,f(x)=ex(x-2),f′(x)=ex+ex(x-2)=ex(x-1),当x∈(0,2)时,f′(x)>f′(0)=-1,因此D是假命题.


科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,已知椭圆 ![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ![]() ,长轴长为4,过椭圆的左顶点A作直线l,分别交椭圆和圆x2+y2=a2于相异两点P,Q.
,长轴长为4,过椭圆的左顶点A作直线l,分别交椭圆和圆x2+y2=a2于相异两点P,Q. 
(1)若直线l的斜率为 ![]() ,求
,求 ![]() 的值;
的值;
(2)若 ![]() =λ
=λ ![]() ,求实数λ的取值范围.
,求实数λ的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公园准备在一圆形水池里设置两个观景喷泉,观景喷泉的示意图如图所示,A,B两点为喷泉,圆心O为AB的中点,其中OA=OB=a米,半径OC=10米,市民可位于水池边缘任意一点C处观赏. 
(1)若当∠OBC= ![]() 时,sin∠BCO=
时,sin∠BCO= ![]() ,求此时a的值;
,求此时a的值;
(2)设y=CA2+CB2 , 且CA2+CB2≤232.
(i)试将y表示为a的函数,并求出a的取值范围;
(ii)若同时要求市民在水池边缘任意一点C处观赏喷泉时,观赏角度∠ACB的最大值不小于 ![]() ,试求A,B两处喷泉间距离的最小值.
,试求A,B两处喷泉间距离的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,以原点O为顶点,以y轴为对称轴的抛物线E的焦点为F(0,1),点M是直线l:y=m(m<0)上任意一点,过点M引抛物线E的两条切线分别交x轴于点S,T,切点分别为B,A.
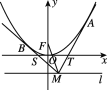
(1)求抛物线E的方程;
(2)求证:点S,T在以FM为直径的圆上.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在如图所示的四棱锥P﹣ABCD中,四边形ABCD为正方形,PA⊥CD,BC⊥平面PAB,且E,M,N分别为PD,CD,AD的中点, ![]() =3
=3 ![]() .
. 
(1)证明:PB∥平面FMN;
(2)若PA=AB,求二面角E﹣AC﹣B的余弦值. 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,椭圆 ![]() =1(a>b>0)的左、右顶点分别为A,B,焦距为2
=1(a>b>0)的左、右顶点分别为A,B,焦距为2 ![]() ,直线x=﹣a与y=b交于点D,且|BD|=3
,直线x=﹣a与y=b交于点D,且|BD|=3 ![]() ,过点B作直线l交直线x=﹣a于点M,交椭圆于另一点P.
,过点B作直线l交直线x=﹣a于点M,交椭圆于另一点P. 
(1)求椭圆的方程;
(2)证明: ![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是一次考试成绩的样本频率分布直方图(样本容量n=200),若成绩不低于60分为及格,则样本中的及格人数是( )

A. 6 B. 36 C. 60 D. 120
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com