直线y=kx与圆x2+y2-6x-4y+10=0相交于两个不同点A、B,当k取不同实数值时,求AB中点的轨迹方程.
【答案】
分析:法一为参数法,适当引入参数,设出中点坐标,通过联立方程组,利用韦达定理,再消去参数得所求轨迹;
法二为“差分法”,设出A(x
1,y
1),B(x
2,y
2),代入圆的方程,作差,利用中点公式,结合直线的斜率,消去参数求中点轨迹方程.
解答:解:法一:由
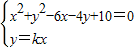
消去y,得(1+k
2)x
2-(6+4k)x+10=0.
设此方程的两根为x
1、x
2,AB的中点坐标为P(x,y),
则由韦达定理和中点坐标公式,得x=
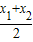
=
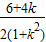
=
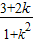
.①
又点P在直线y=kx上,
∴y=kx.
∴k=
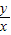
.②
将②代入①,得x=
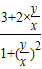
(x≠0),整理得x
2+y
2-3x-2y=0.
故轨迹是圆x
2+y
2-3x-2y=0位于已知圆内的部分.
解法二:设A(x
1,y
1),B(x
2,y
2),则
x
12+y
12-6x
1-4y
1+10=0,①
x
22+y
22-6x
2-4y
2+10=0,②
①-②,得(x
12-x
22)+(y
12-y
22)-6(x
1-x
2)-4(y
1-y
2)=0.
设AB的中点为(x,y),则x
1+x
2=2x,y
1+y
2=2y.
代入上式,有2x(x
1-x
2)+2y(y
1-y
2)-6(x
1-x
2)-4(y
1-y
2)=0,
即(2x-6)(x
1-x
2)+(2y-4)(y
1-y
2)=0.
∴
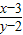
=-
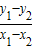
=-k.③
又∵y=kx,④
由③④得x
2+y
2-3x-2y=0.
故所求轨迹为已知圆内的一段弧.
点评:本题考查与圆有关的轨迹问题.法一为参数法,适当引入参数,再消去参数得所求轨迹;法二为“差分法”,是求中点轨迹的一种常用方法.

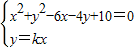
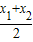 =
=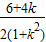 =
=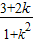 .①
.①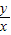 .②
.②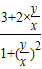 (x≠0),整理得x2+y2-3x-2y=0.
(x≠0),整理得x2+y2-3x-2y=0.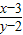 =-
=-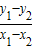 =-k.③
=-k.③

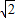 与圆x2+y2=2相交于P、Q两点,且∠POQ=120°(其中O为原点),k的值为 .
与圆x2+y2=2相交于P、Q两点,且∠POQ=120°(其中O为原点),k的值为 .