
 -1|.
-1|. 的图象经过怎样的变换可以得到函数y=f(x)的图象,并作出函数y=f(x)的图象;
的图象经过怎样的变换可以得到函数y=f(x)的图象,并作出函数y=f(x)的图象; ≤x≤2},B=[0,1],试判断A与B的关系;
≤x≤2},B=[0,1],试判断A与B的关系; 的图象向下平移1个单位,再将所得图象位于 x轴下方的部分翻折到x轴上方即可得y=f(x)的图象.
的图象向下平移1个单位,再将所得图象位于 x轴下方的部分翻折到x轴上方即可得y=f(x)的图象.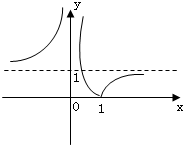 …3’
…3’ ≤x≤2时,0≤f(x)≤1,所以A=[0,1]=B …8’
≤x≤2时,0≤f(x)≤1,所以A=[0,1]=B …8’ 与a<b矛盾 …12’
与a<b矛盾 …12’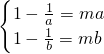 可知mx2-x+1=0在[1,+∞)内有两不等实根
可知mx2-x+1=0在[1,+∞)内有两不等实根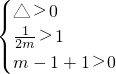 ,得
,得
 …16’
…16’

 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案科目:高中数学 来源: 题型:
| π |
| 4 |
| π |
| 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| x |
| m |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| f(n) |
A、
| ||
B、
| ||
C、
| ||
D、
|
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com