Question

【题目】已知命题p：x∈（-2，1），使等式x2-x-m=0成立，命题q：表示椭圆．

（1）若命题p为真命题，求实数m的取值范围．

（2）判断命题p为真命题是命题q为真命题的什么条件（请用简要过程说明是“充分不必要条件”、“必要不充分条件”、“充要条件”和“既不充分也不必要条件”中的哪一个）

Answer 1

【答案】（1）{m|≤m＜6}（2）p是q的必要不充分条件

【解析】

（1）把：x∈（-2，1），使等式x2-x-m=0成立转化为方程x2-x-m=0在（-2，1）上有解，即m的取值范围就是函数y=x2-x在（-2，1）上的值域，再求二次函数的值域得答案；

（2）由表示椭圆求得m的范围，利用集合间的关系结合充分必要条件的判定得答案．

解：（1）由题意，方程x2-x-m=0在（-2，1）上有解，

即m的取值范围就是函数y=x2-x在（-2，1）上的值域，

函数y=x2-x的对称轴方程为x=，

则当x=时，有最小值为，

当x=-2时，有最大值为6．

可得{m|≤m＜6}；

（2）∵命题q：表示椭圆为真命题，

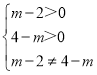∴，解得2＜m＜3或3＜m＜4．

故有{m|≤m＜6}{m|2＜m＜3或3＜m＜4}．

∴p是q的必要不充分条件．