
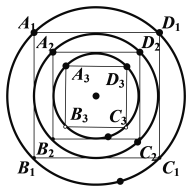
【题目】如图,内接于圆![]() 的正方形
的正方形![]() 边长为1,圆
边长为1,圆![]() 内切于正方形
内切于正方形![]() ,正方形
,正方形![]() 内接于圆
内接于圆![]() ,···,正方形
,···,正方形![]() 内接于圆
内接于圆![]() ,圆
,圆![]() 内切于正方形
内切于正方形![]() ,正方形
,正方形![]() 内接于圆
内接于圆![]() ,由此无穷个步骤进行下去记圆
,由此无穷个步骤进行下去记圆![]() 的面积记作
的面积记作![]() ,记正方形
,记正方形![]() 的面积记作
的面积记作![]() .
.
(1)求![]() 的值
的值
(2)记![]() 的所有项和为
的所有项和为![]() ,
,![]() 的所有项和为
的所有项和为![]() ,求
,求![]() 的值.
的值.
 一本好题口算题卡系列答案
一本好题口算题卡系列答案科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 上在第一象限内的点H(1,t)到焦点F的距离为2.
上在第一象限内的点H(1,t)到焦点F的距离为2.
(1)若![]() ,过点M,H的直线与该抛物线相交于另一点N,求
,过点M,H的直线与该抛物线相交于另一点N,求![]() 的值;
的值;
(2)设A、B是抛物线E上分别位于x轴两侧的两个动点,且![]() (其中O为坐标原点).
(其中O为坐标原点).
①求证:直线AB必过定点,并求出该定点Q的坐标;
②过点Q作AB的垂线与该抛物线交于G、D两点,求四边形AGBD面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图给出的是某高校土木工程系大四年级55名学生期末考试专业成绩的频率分布折线图(连接频率分布直方图中各小长方形上端的中点),其中组距为10,且本次考试中最低分为50分,最高分为100分.根据图中所提供的信息,则下列结论中正确的是( )

A. 成绩是75分的人数有20人
B. 成绩是100分的人数比成绩是50分的人数多
C. 成绩落在70-90分的人数有35人
D. 成绩落在75-85分的人数有35人
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}为等比数列, ![]() 公比为
公比为![]()
![]() 为数列{an}的前n项和.
为数列{an}的前n项和.
(1)若![]() 求
求![]() ;
;
(2)若调换![]() 的顺序后能构成一个等差数列,求
的顺序后能构成一个等差数列,求![]() 的所有可能值;
的所有可能值;
(3)是否存在正常数![]() ,使得对任意正整数n,不等式
,使得对任意正整数n,不等式![]() 总成立?若存在,求出
总成立?若存在,求出![]() 的范围,若不存在,请说明理由.
的范围,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线x2=4y的焦点F和点A(-1,8),点P为抛物线上一点,则|PA|+|PF|的最小值为( )
A. 16 B. 6 C. 12 D. 9
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]()
![]() ,点P为直线l:
,点P为直线l:![]() 上且不在x轴上的任意一点,直线
上且不在x轴上的任意一点,直线![]() 和
和![]() 与椭圆的交点分别为A、B和C、D、O为坐标原点.
与椭圆的交点分别为A、B和C、D、O为坐标原点.
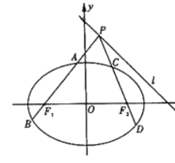
(1)求![]() 的周长;
的周长;
(2)设直线![]()
![]() 的斜线分别为
的斜线分别为![]()
![]() ,证明:
,证明:![]() ;
;
(3)问直线l上是否存在点P,使得直线OA、OB、OC、OD的斜率![]() 满足
满足![]() ?若存在,求出所有满足条件的点P的坐标;若不存在,说明理由.
?若存在,求出所有满足条件的点P的坐标;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合![]() ,函数
,函数![]() 定义于
定义于![]() 并取值于
并取值于![]() .(用数字作答)
.(用数字作答)
(1)若![]() 对于任意的
对于任意的![]() 成立,则这样的函数
成立,则这样的函数![]() 有_______个;
有_______个;
(2)若至少存在一个![]() ,使
,使![]() ,则这样的函数
,则这样的函数![]() 有____个.
有____个.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我们要计算由抛物线![]() ,x轴以及直线
,x轴以及直线![]() 所围成的区域的面积S,可用x轴上的分点
所围成的区域的面积S,可用x轴上的分点![]() 、
、![]() 、
、![]() 、…、
、…、![]() 、1将区间
、1将区间![]() 分成n个小区间,在每个小区间上做一个小矩形,使矩形的左端点在抛物线
分成n个小区间,在每个小区间上做一个小矩形,使矩形的左端点在抛物线![]() 上,这些矩形的高分别为
上,这些矩形的高分别为![]() 、
、![]() 、
、![]() 、…、
、…、![]() ,矩形的底边长都是
,矩形的底边长都是![]() ,设所有这些矩形面积的总和为
,设所有这些矩形面积的总和为![]() ,为求S,只须令分割的份数n无限增大,
,为求S,只须令分割的份数n无限增大,![]() 就无限趋近于S,即
就无限趋近于S,即![]() .
.
(1)求数列![]() 的通项公式,并求出S;
的通项公式,并求出S;
(2)利用相同的思想方法,探求由函数![]()
![]() 的图象,x轴以及直线
的图象,x轴以及直线![]() 和
和![]() 所围成的区域的面积T.
所围成的区域的面积T.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com