
【题目】设数列![]() 满足
满足![]() ,其中A,B是两个确定的实数,
,其中A,B是两个确定的实数,![]()
(1)若![]() ,求
,求![]() 的前n项和;
的前n项和;
(2)证明:![]() 不是等比数列;
不是等比数列;
(3)若![]() ,数列
,数列![]() 中除去开始的两项外,是否还有相等的两项,并证明你的结论.
中除去开始的两项外,是否还有相等的两项,并证明你的结论.
 全优测试卷系列答案
全优测试卷系列答案 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案科目:高中数学 来源: 题型:
【题目】随着金融市场的发展,越来越多人选择投资“黄金”作为理财的手段,下面将A市把黄金作为理财产品的投资人的年龄情况统计如下图所示.
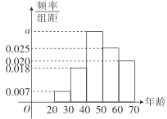
(1)求把黄金作为理财产品的投资者的年龄的中位数;(结果用小数表示,小数点后保留两位有效数字)
(2)现按照分层抽样的方法从年龄在![]() 和
和![]() 的投资者中随机抽取5人,再从这5人中随机抽取3人进行投资调查,求恰有1人年龄在
的投资者中随机抽取5人,再从这5人中随机抽取3人进行投资调查,求恰有1人年龄在![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
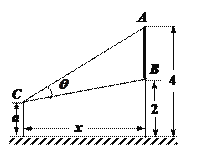
【题目】如图,墙上有一壁画,最高点![]() 离地面4米,最低点
离地面4米,最低点![]() 离地面2米,观察者从距离墙
离地面2米,观察者从距离墙![]() 米,离地面高
米,离地面高![]() 米的
米的![]() 处观赏该壁画,设观赏视角
处观赏该壁画,设观赏视角![]()
(1)若![]() 问:观察者离墙多远时,视角
问:观察者离墙多远时,视角![]() 最大?
最大?
(2)若![]() 当
当![]() 变化时,求
变化时,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
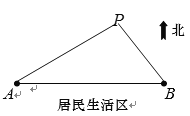
【题目】如图所示,![]() 、
、![]() 是两个垃圾中转站,
是两个垃圾中转站,![]() 在
在![]() 的正东方向
的正东方向![]() 千米处,
千米处,![]() 的南面为居民生活区.为了妥善处理生活垃圾,政府决定在
的南面为居民生活区.为了妥善处理生活垃圾,政府决定在![]() 的北面建一个垃圾发电厂
的北面建一个垃圾发电厂![]() .垃圾发电厂
.垃圾发电厂![]() 的选址拟满足以下两个要求(
的选址拟满足以下两个要求(![]() 、
、![]() 、
、![]() 可看成三个点):①垃圾发电厂到两个垃圾中转站的距离与它们每天集中的生活垃圾量成反比,比例系数相同;②垃圾发电厂应尽量远离居民区(这里参考的指标是点
可看成三个点):①垃圾发电厂到两个垃圾中转站的距离与它们每天集中的生活垃圾量成反比,比例系数相同;②垃圾发电厂应尽量远离居民区(这里参考的指标是点![]() 到直线
到直线![]() 的距离要尽可能大).现估测得
的距离要尽可能大).现估测得![]() 、
、![]() 两个中转站每天集中的生活垃圾量分别约为
两个中转站每天集中的生活垃圾量分别约为![]() 吨和
吨和![]() 吨.设
吨.设![]() .
.
(1)求![]() (用
(用![]() 的表达式表示);
的表达式表示);
(2)垃圾发电厂该如何选址才能同时满足上述要求?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列判断正确的是( )
A.若随机变量![]() 服从正态分布
服从正态分布![]() ,
,![]() ,则
,则![]() ;
;
B.已知直线![]() 平面
平面![]() ,直线
,直线![]() 平面
平面![]() ,则“
,则“![]() ”是“
”是“![]() ”的充分不必要条件;
”的充分不必要条件;
C.若随机变量![]() 服从二项分布:
服从二项分布:![]() ,则
,则![]() ;
;
D.![]() 是
是![]() 的充分不必要条件.
的充分不必要条件.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() .
.
(1)当![]() 时,对于一切
时,对于一切![]() ,函数
,函数![]() 在区间
在区间![]() 内总存在唯一零点,求
内总存在唯一零点,求![]() 的取值范围;
的取值范围;
(2)若![]() 区间
区间![]() 上是单调函数,求
上是单调函数,求![]() 的取值范围;
的取值范围;
(3)当![]() ,
,![]() 时,函数
时,函数![]() 在区间
在区间![]() 内的零点为
内的零点为![]() ,判断数列
,判断数列![]() ,
,![]() ,…,
,…,![]() ,…的增减性,并说明理由.
,…的增减性,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一次猜奖游戏中,1,2,3,4四扇门里摆放了![]() ,
,![]() ,
,![]() ,
,![]() 四件奖品(每扇门里仅放一件).甲同学说:1号门里是
四件奖品(每扇门里仅放一件).甲同学说:1号门里是![]() ,3号门里是
,3号门里是![]() ;乙同学说:2号门里是
;乙同学说:2号门里是![]() ,3号门里是
,3号门里是![]() ;丙同学说:4号门里是
;丙同学说:4号门里是![]() ,2号门里是
,2号门里是![]() ;丁同学说:4号门里是
;丁同学说:4号门里是![]() ,3号门里是
,3号门里是![]() .如果他们每人都猜对了一半,那么4号门里是( )
.如果他们每人都猜对了一半,那么4号门里是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com