
【题目】如图,三棱柱ABC﹣A1B1C1中,侧面BB1C1C为菱形,B1C的中点为O,且AO⊥平面BB1C1C. 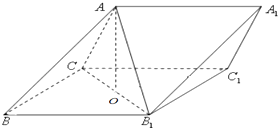
(1)证明:B1C⊥AB;
(2)若AC⊥AB1 , ∠CBB1=60°,BC=2,求B1到平面ABC的距离.
【答案】
(1)证明:连结BC1,则BC1与B1C交于O,
∵侧面BB1C1C为菱形,∴B1C⊥BC1,
∵AO⊥平面BB1C1C,∴B1C⊥AO
又∵BC1∩AO=O,
∴B1C⊥平面ABO,
由于AB平面ABO,∴B1C⊥AB

(2)解:设点B1 到平面ABC 的距离为h,
∵侧面BB1C1C为菱形,∠CBB1=60°,BC=2,
∴△CBB1为等边三角形,
∴BC=BB1=B1C=2,BO= ![]()
∵AC⊥AB1,∴ ![]() ,
,
Rt△AOB中,AB= ![]() =2
=2
∴S△ABC= ![]() =
= ![]() ,
,
∵ ![]() =
= ![]() ,
,
∴ ![]() ,
,
∴h= ![]() .
.
∴点B1 到平面ABC 的距离为 ![]()
【解析】(1)要证B1C⊥AB,即证B1C⊥平面ABC1 , 由菱形的对角线垂直和线面垂直的性质,即可得证;(2)由棱锥的体积公式,利用 ![]() =
= ![]() ,即可得到B1到平面ABC的距离.
,即可得到B1到平面ABC的距离.


 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:高中数学 来源: 题型:
【题目】已知f(x)=sin(x+1) ![]() ﹣
﹣ ![]() cos(x+1)
cos(x+1) ![]() ,则f(1)+f(2)+f(3)+…+f(2011)=( )
,则f(1)+f(2)+f(3)+…+f(2011)=( )
A.2 ![]()
B.![]()
C.﹣ ![]()
D.0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】自然数按如图的规律排列:则上起第2007行左起2008列的数为( ) 
A.20072
B.20082
C.2006×2007
D.2007×2008
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥V﹣ABC中,平面VA B⊥平面 ABC,AC=BC,O,M分别为A B,VA的中点. 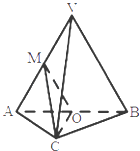
(1)求证:VB∥平面 M OC;
(2)求证:平面MOC⊥平面VAB.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,将自然数按如下规则“放置”在平面直角坐标系中,使其满足条件:①每个自然数“放置”在一个“整点”(横纵坐标均为整数的点)上;②0在原点,1在(0,1)点,2在(1,1)点,3在(1,0)点,4在(1,﹣1)点,5在(0,﹣1)点,…,即所有自然数按顺时针“缠绕”在以“0”为中心的“桩”上,则放置数字(2n+1)2 , n∈N*的整点坐标是 . 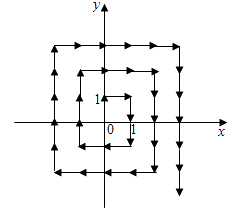
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C过点M(0,﹣2),N(3,1),且圆心C在直线x+2y+1=0上.
(1)求圆C的方程;
(2)问是否存在满足以下两个条件的直线l:①斜率为1;②直线被圆C截得的弦为AB,以AB为直径的圆C1过原点.若存在这样的直线,请求出其方程;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某次测验中,有6位同学的平均成绩为75分.用xn表示编号为n(n=1,2,…,6)的同学所得成绩,且前5位同学的成绩如下:
编号n | 1 | 2 | 3 | 4 | 5 |
成绩xn | 70 | 76 | 72 | 70 | 72 |
(1)求第6位同学的成绩x6 , 及这6位同学成绩的标准差s;
(2)从前5位同学中,随机地选2位同学,求恰有1位同学成绩在区间(68,75)中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 和直线
和直线![]() :
: ![]() ,椭圆的离心率
,椭圆的离心率![]() ,坐标原点到直线
,坐标原点到直线![]() 的距离为
的距离为![]() .
.

(Ⅰ)求椭圆的方程;
(Ⅱ)已知定点![]() ,若直线
,若直线![]() 过点
过点![]() 且与椭圆相交于
且与椭圆相交于![]() 两点,试判断是否存在直线
两点,试判断是否存在直线![]() ,使以
,使以![]() 为直径的圆过点
为直径的圆过点![]() ?若存在,求出直线
?若存在,求出直线![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,A(a,0)(a>0),B(0,a),C(﹣4,0),D(0,4)设△AOB的外接圆圆心为E. 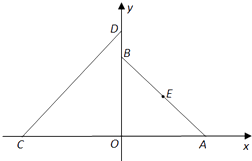
(1)若⊙E与直线CD相切,求实数a的值;
(2)设点P在圆E上,使△PCD的面积等于12的点P有且只有三个,试问这样的⊙E是否存在,若存在,求出⊙E的标准方程;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com