
| A. | $[-\frac{{\sqrt{2}}}{4},\frac{{\sqrt{2}}}{4}]$ | B. | $[-\frac{1}{4},\frac{1}{4}]$ | C. | $[-\frac{{\sqrt{2}}}{2},\frac{{\sqrt{2}}}{2}]$ | D. | $[-\frac{1}{2},\frac{1}{2}]$ |
分析 把x≥0时的f(x)改写成分段函数,求出其最小值,由函数的奇偶性可得x<0时的函数的最大值,由对?x∈R,都有f(x-1)≤f(x),可得4a2-(-4a2)≤1,求解该不等式得答案.
解答 解:当x≥0时,
f(x)=$\left\{\begin{array}{l}{\frac{1}{2}(x-4{a}^{2}),x≥{a}^{2}}\\{\frac{1}{2}(-x-2{a}^{2}),0≤x<{a}^{2}}\end{array}\right.$,
由f(x)=$\frac{1}{2}(x-4{a}^{2})$,x≥a2,得f(x)≥-$\frac{3}{2}$a2;
由f(x)=$\frac{1}{2}(-x-2{a}^{2})$,0≤x<a2,得f(x)>-$\frac{3}{2}$a2.
∴当x≥0时,$f(x)_{min}=-\frac{3}{2}{a}^{2}$.
∵函数f(x)为奇函数,
∴当x<0时,$f(x)_{max}=\frac{3}{2}{a}^{2}$.
∵对?x∈R,都有f(x-1)≤f(x),如图,
∴4a2-(-4a2)≤1,即8a2≤1,解得:-$\frac{\sqrt{2}}{4}$≤a≤$\frac{\sqrt{2}}{4}$.
∴实数a的取值范围是[-$\frac{\sqrt{2}}{4}$,$\frac{\sqrt{2}}{4}$].
故选:A.
点评 本题考查了恒成立问题,考查了函数奇偶性的性质,运用了数学转化思想方法,解答此题的关键是由对?x∈R,都有f(x-1)≤f(x)得到不等式4a2-(-4a2)≤1,是中档题.


 学业测评一课一测系列答案
学业测评一课一测系列答案 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $y=±\frac{{\sqrt{2}}}{2}x$ | B. | $y=±\sqrt{2}x$ | C. | y=±2x | D. | $y=±\frac{1}{2}x$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
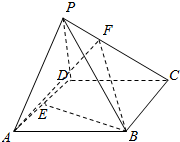 如图所示,P为?ABCD所在平面外一点,E为AD的中点,F为PC上一点,当PA∥平面EBF时,$\frac{PF}{FC}$=$\frac{1}{2}$.
如图所示,P为?ABCD所在平面外一点,E为AD的中点,F为PC上一点,当PA∥平面EBF时,$\frac{PF}{FC}$=$\frac{1}{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com