
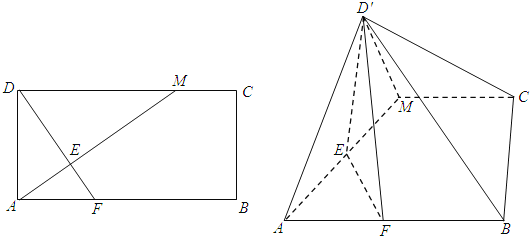
【题目】如图,在矩形ABCD中,![]() ,点M在边DC上,点F在边AB上,且
,点M在边DC上,点F在边AB上,且![]() ,垂足为E,若将
,垂足为E,若将![]() 沿AM折起,使点D位于
沿AM折起,使点D位于![]() 位置,连接
位置,连接![]() ,
,![]() 得四棱锥
得四棱锥![]() .
.
![]() Ⅰ
Ⅰ![]() 求证:
求证:![]() ;
;
![]() Ⅱ
Ⅱ![]() 若
若![]() ,直线
,直线![]() 与平面ABCM所成角的大小为
与平面ABCM所成角的大小为![]() ,求直线
,求直线![]() 与平面ABCM所成角的正弦值.
与平面ABCM所成角的正弦值.
科目:高中数学 来源: 题型:
【题目】(本小题13分)已知数列![]() 满足:
满足:![]() ,
,![]() ,且
,且![]()
![]() .记
.记
集合![]() .
.
(Ⅰ)若![]() ,写出集合
,写出集合![]() 的所有元素;
的所有元素;
(Ⅱ)若集合![]() 存在一个元素是3的倍数,证明:
存在一个元素是3的倍数,证明:![]() 的所有元素都是3的倍数;
的所有元素都是3的倍数;
(Ⅲ)求集合![]() 的元素个数的最大值.
的元素个数的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司计划购买1台机器,该种机器使用三年后即被淘汰.机器有一易损零件,在购进机器时,可以额外购买这种零件作为备件,每个200元.在机器使用期间,如果备件不足再购买,则每个500元.现需决策在购买机器时应同时购买几个易损零件,为此搜集并整理了100台这种机器在三年使用期内更换的易损零件数,得下面柱状图.

记![]() 表示
表示![]() 台机器在三年使用期内需更换的易损零件数,
台机器在三年使用期内需更换的易损零件数,![]() 表示
表示![]() 台机器在购买易损零件上所需的费用(单位:元),
台机器在购买易损零件上所需的费用(单位:元),![]() 表示购机的同时购买的易损零件数.
表示购机的同时购买的易损零件数.
(1)若![]() ,求
,求![]() 与
与![]() 的函数解析式;
的函数解析式;
(2)若要求 “需更换的易损零件数不大于![]() ”的频率不小于
”的频率不小于![]() ,求
,求![]() 的最小值;
的最小值;
(3)假设这![]() 台机器在购机的同时每台都购买
台机器在购机的同时每台都购买![]() 个易损零件,或每台都购买
个易损零件,或每台都购买![]() 个易损零件,分别计算这
个易损零件,分别计算这![]() 台机器在购买易损零件上所需费用的平均数,以此作为决策依据,购买
台机器在购买易损零件上所需费用的平均数,以此作为决策依据,购买![]() 台机器的同时应购买
台机器的同时应购买![]() 个还是
个还是![]() 个易损零件?
个易损零件?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
以直角坐标系xOy的原点为极点,x轴的非负半轴为极轴建立极坐标系,且两坐标系相同的长度单位.已知点N的极坐标为( ![]() ,
, ![]() ),M是曲线C1:ρ=1上任意一点,点G满足
),M是曲线C1:ρ=1上任意一点,点G满足 ![]() ,设点G的轨迹为曲线C2 .
,设点G的轨迹为曲线C2 .
(1)求曲线C2的直角坐标方程;
(2)若过点P(2,0)的直线l的参数方程为  (t为参数),且直线l与曲线C2交于A,B两点,求
(t为参数),且直线l与曲线C2交于A,B两点,求 ![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
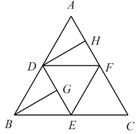
【题目】如图,在边长为4的正三角形ABC中,D,E,F分别为各边的中点,G,H分别为DE,AF的中点,将![]() 沿DE,EF,DF折成正四面体
沿DE,EF,DF折成正四面体![]() ,则在此正四面体中,下列说法正确的是______.
,则在此正四面体中,下列说法正确的是______.
![]() 异面直线PG与DH所成的角的余弦值为
异面直线PG与DH所成的角的余弦值为![]() ;
;
![]() ;
;
![]() 与PD所成的角为
与PD所成的角为![]() ;
;
![]() 与EF所成角为
与EF所成角为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将参加夏令营的600名学生编号为:001,002,…,600,采用系统抽样的方法抽取一个容量为50的样本,且随机抽得的编号为003.这600名学生分住在3个营区,从001到300住在第1营区,从301到495住在第2营区,从496到600住在第3营区,则3个营区被抽中的人数依次为( )
A. 26,16,8 B. 25,16,9
C. 25,17,8 D. 24,17,9
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}满足a3=2,前3项和为S3=![]() .
.
(1)求{an}的通项公式;
(2)设等比数列{bn}满足b1=a1,b4=a15,求{bn}的前n项和Tn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l: ![]() (t为参数,α为l的倾斜角),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C为:ρ2﹣6ρcosθ+5=0.
(t为参数,α为l的倾斜角),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C为:ρ2﹣6ρcosθ+5=0.
(1)若直线l与曲线C相切,求α的值;
(2)设曲线C上任意一点的直角坐标为(x,y),求x+y的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com