
【题目】已知向量 ![]() =(ex , lnx+k),
=(ex , lnx+k), ![]() =(1,f(x)),
=(1,f(x)), ![]() ∥
∥ ![]() (k为常数,e是自然对数的底数),曲线y=f(x)在点(1,f(1))处的切线与y轴垂直,F(x)=xexf′(x).
(k为常数,e是自然对数的底数),曲线y=f(x)在点(1,f(1))处的切线与y轴垂直,F(x)=xexf′(x).
(1)求k的值及F(x)的单调区间;
(2)已知函数g(x)=﹣x2+2ax(a为正实数),若对任意x2∈[0,1],总存在x1∈(0,+∞),使得g(x2)<F(x1),求实数a的取值范围.
【答案】
(1)解:由已知可得:f(x)= ![]() ,
,
∴ ![]() ,
,
由已知, ![]() ,
,
∴k=1
∴F(x)=xexf'(x)= ![]() ,
,
所以F'(x)=﹣lnx﹣2
由 ![]() ,
,
由 ![]()
∴F(x)的增区间为 ![]() ,减区间为
,减区间为 ![]()
(2)解:∵对于任意x2∈[0,1],总存在x1∈(0,+∞),使得g(x2)<F(x1),
∴g(x)max<F(x)max…(6分)
由(I)知,当 ![]() 时,F(x)取得最大值
时,F(x)取得最大值 ![]() .
.
对于g(x)=﹣x2+2ax,其对称轴为x=a
当0<a≤1时, ![]() ,
,
∴ ![]() ,从而0<a≤1
,从而0<a≤1
当a>1时,g(x)max=g(1)=2a﹣1,
∴ ![]() ,从而
,从而 ![]()
综上可知: ![]()
【解析】(1)利用向量平行的条件求出函数y=f(x),再求出此函数的导函数,函数在点(1,f(1))处的切线与x轴平行,说明f′(1)=0,则k值可求;从而得出F(x)的解析式,求出函数F(x)的定义域,然后让导函数等于0求出极值点,借助于导函数在各区间内的符号求函数F(x)的单调区间.(2)对于任意x2∈[0,1],总存在x1∈(0,+∞),使得g(x2)<F(x1),等价于g(x)max<F(x)max , 再求得F(x)取得最大值;利用二次函数的图象,对a进行分类讨论,得出g(x)在[0,1]上的最大值,由g(x)在[0,1]上的最大值小于F(x)max得a的范围,结合分类时a的范围得a的取值范围.
【考点精析】关于本题考查的利用导数研究函数的单调性,需要了解一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减才能得出正确答案.
在这个区间单调递减才能得出正确答案.


科目:高中数学 来源: 题型:
【题目】在四棱锥P﹣ABCD中,各侧面是全等的等腰三角形,腰长为4且顶角为30°,底面是正方形(如图),在棱PB,PC上各有一点M,N,且四边形AMND的周长最小,点S从A出发依次沿四边形AM,MN,ND运动至点D,记点S行进的路程为x,棱锥S﹣ABCD的体积为V(x),则函数V(x)的图象是( ) 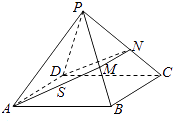
A.
B.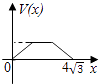
C.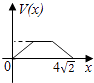
D.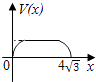
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sin(π﹣2x),g(x)=2cos2x,则下列结论正确的是( )
A.函数f(x)在区间[ ![]() ]上为增函数
]上为增函数
B.函数y=f(x)+g(x)的最小正周期为2π
C.函数y=f(x)+g(x)的图象关于直线x= ![]() 对称
对称
D.将函数f(x)的图象向右平移 ![]() 个单位,再向上平移1个单位,得到函数g(x)的图象
个单位,再向上平移1个单位,得到函数g(x)的图象
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个透明密闭的正方体容器中,恰好盛有该容器一半容积的水,任意转动这个正方体,则水面在容器中的形状可以是:
①三角形;②矩形;③正方形;④正六边形.
其中正确的结论是(把你认为正确的序号都填上)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() 的定义域为
的定义域为![]() ,如果存在正实数
,如果存在正实数![]() ,使得对任意
,使得对任意![]() ,都有
,都有![]() ,且
,且![]() 恒成立,则称函数
恒成立,则称函数![]() 为
为![]() 上的“
上的“![]() 的型增函数”,已知
的型增函数”,已知![]() 是定义在
是定义在![]() 上的奇函数,且在
上的奇函数,且在![]() 时,
时, ![]() ,若
,若![]() 为
为![]() 上的“2017的型增函数”,则实数
上的“2017的型增函数”,则实数![]() 的取值范围是__________.
的取值范围是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,AB是圆O的直径,C是圆O上不同于A,B的一点,PA⊥平面ABC,E是PC的中点, ![]() ,PA=AC=1.
,PA=AC=1. 
(1)求证:AE⊥PB;
(2)求二面角A﹣PB﹣C的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线y=Asin(wx+φ)(A>0,w>0)上的一个最高点的坐标为( ![]() ,
, ![]() ),由此点到相邻最低点间的曲线与x轴交于点(
),由此点到相邻最低点间的曲线与x轴交于点( ![]() π,0),φ∈(﹣
π,0),φ∈(﹣ ![]() ,
, ![]() ).
).
(1)求这条曲线的函数解析式;
(2)求函数的单调增区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn , 且Sn=4an﹣3(n∈N*).
(Ⅰ)证明:数列{an}是等比数列;
(Ⅱ)若数列{bn}满足bn+1=an+bn(n∈N*),且b1=2,求数列{bn}的通项公式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱柱ABC﹣A1B1C1中,侧棱AA1⊥平面ABC,△ABC为等腰直角三角形,∠BAC=90°,且AB=AA1=1,E,F分别是CC1 , BC的中点.
(Ⅰ)求证:B1F⊥平面AEF;
(Ⅱ)求三棱锥E﹣AB1F的体积.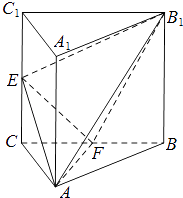
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com