
【题目】有以下命题:
①如果向量 ![]() ,
, ![]() 与任何向量不能构成空间向量的一组基底,那么
与任何向量不能构成空间向量的一组基底,那么 ![]() ,
, ![]() 的关系是不共线;
的关系是不共线;
②O,A,B,C为空间四点,且向量 ![]() ,
, ![]() ,
, ![]() 不构成空间的一个基底,则点O,A,B,C一定共面;
不构成空间的一个基底,则点O,A,B,C一定共面;
③已知向量 ![]() ,
, ![]() ,
, ![]() 是空间的一个基底,则向量
是空间的一个基底,则向量 ![]() +
+ ![]() ,
, ![]() ﹣
﹣ ![]() ,
, ![]() 也是空间的一个基底;
也是空间的一个基底;
④△ABC中,A>B的充要条件是sinA>sinB.
其中正确的命题个数是( )
A.1
B.2
C.3
D.4
【答案】C
【解析】解:对于①,如果向量 ![]() ,
, ![]() 与任何向量不能构成空间向量的一组基底,那么
与任何向量不能构成空间向量的一组基底,那么 ![]() ,
, ![]() 的关系是共线,所以不正确.
的关系是共线,所以不正确.
对于②,O,A,B,C为空间四点,且向量 ![]() ,
, ![]() ,
, ![]() 不构成空间的一个基底,那么点O,A,B,C一定共面;这是正确的.
不构成空间的一个基底,那么点O,A,B,C一定共面;这是正确的.
对于③,已知向量 ![]() ,
, ![]() ,
, ![]() 是空间的一个基底,所以因为三个向量非零不共线,则向量
是空间的一个基底,所以因为三个向量非零不共线,则向量 ![]() +
+ ![]() ,
, ![]() ﹣
﹣ ![]() ,
, ![]() 也不共线,也是空间的一个基底,这是正确的.
也不共线,也是空间的一个基底,这是正确的.
对于④,△ABC中,A>Ba>b2RsinA>2RsinBsinA>sinB,所以正确.
故选:C.
【考点精析】通过灵活运用命题的真假判断与应用,掌握两个命题互为逆否命题,它们有相同的真假性;两个命题为互逆命题或互否命题,它们的真假性没有关系即可以解答此题.


科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABC﹣A1B1C1中,侧棱AA1⊥底面ABC,AC=3,BC=4,AB=5,AA1=4,点D是AB的中点. 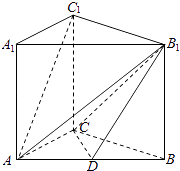
(1)求证:AC1∥平面CDB1
(2)求证:AC⊥BC1
(3)求直线AB1与平面BB1C1C所成的角的正切值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】进行随机抽样时,甲学生认为:“每次抽取一个个体时,任一个个体a被抽到的概率”与“在整个抽样过程中个体a被抽到的概率”是一回事,而学生乙则认为两者不是一回事.你认为甲、乙两学生中哪个对?请列举具体例子加以说明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若a,b是函数f(x)=x2﹣px+q(p>0,q>0)的两个不同的零点,且a,b,﹣2这三个数可适当排序后成等差数列,也可适当排序后成等比数列,则p+q的值等于 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正方体ABCD﹣A1B1C1D1中,M,N,P分别是B1B,B1C1 , CD的中点,则MN与D1P所成角的余弦值为( ) 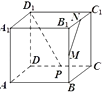
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱锥P﹣ABC中,PB⊥底面ABC,∠BCA=90°,PB=BC=CA=2,E为PC的中点,M为AB的中点,点F在PA上,且2PF=FA. 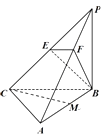
(1)求证:BE⊥平面PAC;
(2)求证:CM∥平面BEF;
(3)求平面ABC与平面BEF所成的二面角的平面角(锐角)的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某食品厂需要定期购买食品配料,该厂每天需要食品配料200千克,配料的价格为1.8元/千克,每次购买配料需支付运费236元,每次购买来的配料还需支付保管费用,其标准如下:7天以内(含7天),无论重量多少,均按10元/天支付;超出7天以外的天数,根据实际剩余配料的重量,以每天0.03元/千克支付.
(1)当9天购买一次配料时,求该厂用于配料的保管费用![]() 是多少元?
是多少元?
(2)设该厂![]() 天购买一次配料,求该厂在这
天购买一次配料,求该厂在这![]() 天中用于配料的总费用
天中用于配料的总费用![]() (元)关于
(元)关于![]() 的函数关系式,并求该厂多少天购买一次配料才能使平均每天支付的费用最少?
的函数关系式,并求该厂多少天购买一次配料才能使平均每天支付的费用最少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABC﹣A1B1C1中,侧棱AA1⊥底面ABC,AB⊥BC,D为AC的中点,AA1=AB=2. 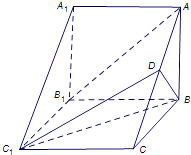
(1)求证:AB1∥平面BC1D;
(2)若BC=3,求三棱锥D﹣BC1C的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某污水处理厂要在一个矩形污水处理池(ABCD)的池底水平铺设污水净化管道(Rt△FHE,H是直角顶点)来处理污水,管道越长,污水净化效果越好.设计要求管道的接口H是AB的中点,E,F分别落在线段BC,AD上.已知AB=20米, ![]() 米,记∠BHE=θ.
米,记∠BHE=θ. 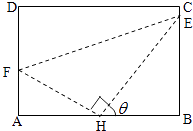
(1)试将污水净化管道的长度L表示为θ的函数,并写出定义域;
(2)若 ![]() ,求此时管道的长度L;
,求此时管道的长度L;
(3)当θ取何值时,污水净化效果最好?并求出此时管道的长度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com