
| A. | $\frac{{\sqrt{3}}}{2}$ | B. | $-\frac{{\sqrt{3}}}{2}$ | C. | $\sqrt{3}$ | D. | 0 |
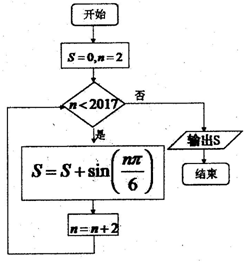
分析 通过依次对n的值判断算法执行,可以看出在算法执行过程中S的值以6为周期周期出现,再由判断框中的条件看出执行的n的最大值是2016,由此即可得到算法输出的正确结果.
解答 解:模拟程序的运行,可得:
S=0,n=2
满足条件n<2017,执行循环体,S=sin$\frac{π}{3}$,n=4,
满足条件n<2017,执行循环体,S=sin$\frac{π}{3}$+sin$\frac{2π}{3}$,n=6,
…
可得程序框图的功能是计算并输出S=sin$\frac{π}{3}$+sin$\frac{2π}{3}$+…+sin$\frac{1008π}{3}$的值.
观察规律可得,算法在执行过程中,S的值以6为周期周期出现,
所以程序共执行了336个周期,所以输出的S值应是0.
故选:D.
点评 本题考查了循环结构中的当型结构,当型结构的特点是当满足条件执行循环,不满足条件跳出循环,算法结束,是基础题.


科目:高中数学 来源: 题型:解答题
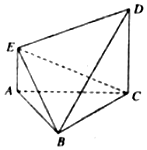 如图,△ABC为边长为2的正三角形,AE∥CD,且AE⊥平面ABC,2AE=CD=2.
如图,△ABC为边长为2的正三角形,AE∥CD,且AE⊥平面ABC,2AE=CD=2.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 一孩 | 二孩 | 合计 | |
| 人民医院 | |||
| 博爱医院 | |||
| 合计 |
| P(k2>k0) | 0.4 | 0.25 | 0.15 | 0.10 |
| k0 | 0.708 | 1.323 | 2.072 | 2.706 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({0,\frac{1}{8}}]$ | B. | $({0,\frac{5}{8}}]$ | C. | $({0,\frac{1}{8}}]∪[{\frac{5}{8},1}]$ | D. | $({0,\frac{1}{8}}]∪[{\frac{1}{4},\frac{5}{8}}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
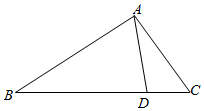 如图,在△ABC中,角A,B,C所对的边为a,b,c,满足sin2A+sin2C-sin2B=$\sqrt{3}$sinA•sinC
如图,在△ABC中,角A,B,C所对的边为a,b,c,满足sin2A+sin2C-sin2B=$\sqrt{3}$sinA•sinC查看答案和解析>>
科目:高中数学 来源: 题型:解答题
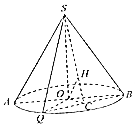 如图,圆锥的横截面为等边三角形SAB,O为底面圆圆心,Q为底面圆周上一点.
如图,圆锥的横截面为等边三角形SAB,O为底面圆圆心,Q为底面圆周上一点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com