
【题目】下面给出了根据我国2012年~2018年水果人均占有量y(单位:kg)和年份代码x绘制的散点图(2012年~2018年的年份代码x分别为1~7).

(1)根据散点图相应数据计算得![]() ,
,![]() ,求y关于x的线性回归方程;
,求y关于x的线性回归方程;
(2)估计我国2023年水果人均占有量是多少?(精确到1kg).
附:回归方程![]() 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为:
 ,
,![]() .
.
科目:高中数学 来源: 题型:
【题目】今年入冬以来,我市天气反复.在下图中统计了我市上个月前15天的气温,以及相对去年同期的气温差(今年气温-去年气温,单位:摄氏度),以下判断错误的是( )
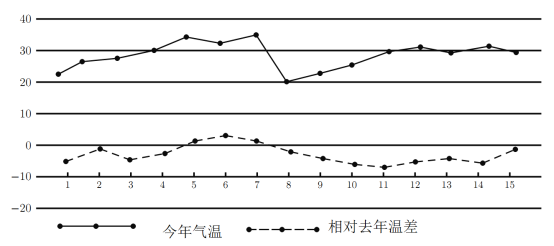
A.今年每天气温都比去年气温低B.今年的气温的平均值比去年低
C.今年8-12号气温持续上升D.今年8号气温最低
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知平面直角坐标系![]() ,直线
,直线![]() 过点
过点![]() ,且倾斜角为
,且倾斜角为![]() ,以
,以![]() 为极点,
为极点,![]() 轴的非负半轴为极轴建立极坐标系,圆
轴的非负半轴为极轴建立极坐标系,圆![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的参数方程和圆
的参数方程和圆![]() 的标准方程;
的标准方程;
(2)设直线![]() 与圆
与圆![]() 交于
交于![]() 、
、![]() 两点,若
两点,若![]() ,求直线
,求直线![]() 的倾斜角的
的倾斜角的![]() 值.
值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为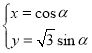 (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)求曲线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)若点![]() 在曲线
在曲线![]() 上,点
上,点![]() 在曲线
在曲线![]() 上,求
上,求![]() 的最小值及此时点
的最小值及此时点![]() 的直角坐标.
的直角坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了缓解城市交通压力,某市市政府在市区一主要交通干道修建高架桥,两端的桥墩现已建好,已知这两桥墩相距m米,“余下的工程”只需建两端桥墩之间的桥面和桥墩.经测算,一个桥墩的工程费用为256万元;距离为x米的相邻两墩之间的桥面工程费用为(2+![]() )x万元.假设桥墩等距离分布,所有桥墩都视为点,且不考虑其他因素.记“余下工程”的费用为y万元.
)x万元.假设桥墩等距离分布,所有桥墩都视为点,且不考虑其他因素.记“余下工程”的费用为y万元.
(1)试写出工程费用y关于x的函数关系式;
(2)当m=640米时,需新建多少个桥墩才能使工程费用y最小?并求出其最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com