
| ax-1 | x+1 |
| ax-1 |
| x+1 |
| 1 |
| a |
|
|
|
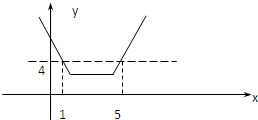 解:(Ⅰ)由
解:(Ⅰ)由| ax-1 |
| x+1 |
| 1 |
| a |
| 1 |
| 3 |
|
|
|
|


 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案科目:高中数学 来源: 题型:
| 2-x+a |
| 1+x |
| g(x) |
| m |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2012•盐城二模)因客流量临时增大,某鞋店拟用一个高为50cm(即EF=50cm)的平面镜自制一个竖直摆放的简易鞋镜.根据经验,一般顾客AB的眼睛B到地面的距离x(cm)在区间[140,180]内.设支架FG高为h(0<h<90)cm,AG=100cm,顾客可视的镜像范围为CD(如图所示),记CD的长度为y(y=GD-GC).
(2012•盐城二模)因客流量临时增大,某鞋店拟用一个高为50cm(即EF=50cm)的平面镜自制一个竖直摆放的简易鞋镜.根据经验,一般顾客AB的眼睛B到地面的距离x(cm)在区间[140,180]内.设支架FG高为h(0<h<90)cm,AG=100cm,顾客可视的镜像范围为CD(如图所示),记CD的长度为y(y=GD-GC).查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
|
| A、0 | B、1 | C、3 | D、2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com