
| A. | ($\frac{π}{6}$,$\frac{π}{4}$) | B. | ($\frac{π}{4}$,$\frac{π}{2}$) | C. | ($\frac{π}{4}$,$\frac{π}{2}$] | D. | ($\frac{π}{4}$,$\frac{π}{3}$] |
分析 由直线l1:y-kx-2和直线l2:2x+y=4联立方程组求出交点坐标,由交点在第一象限,得到横坐标和纵坐标同时大于0,由此能求出k>1,从而能求出直线l1的倾斜角的范围.
解答 解:解方程组$\left\{\begin{array}{l}{y=kx-2}\\{2x+y=4}\end{array}\right.$,得$\left\{\begin{array}{l}{x=\frac{6}{2+k}}\\{y=\frac{4k-4}{2+k}}\end{array}\right.$,
∵直线l1:y-kx-2和直线l2:2x+y=4的交点在第一象限,
∴$\left\{\begin{array}{l}{x=\frac{6}{k+2}>0}\\{y=\frac{4k-4}{2+k}>0}\end{array}\right.$,解得k>1,
∴直线l1的倾斜角的范围是($\frac{π}{4},\frac{π}{2}$).
故选:B.
点评 本题考查直线的倾斜角的范围的求法,是基础题,解题时要认真审题,注意函数与方程思想的合理运用.


科目:高中数学 来源: 题型:选择题
 如图所示为二次函数y=ax2+bx+c的图象,则|OA|•|OB|等于( )
如图所示为二次函数y=ax2+bx+c的图象,则|OA|•|OB|等于( )| A. | $\frac{c}{a}$ | B. | -$\frac{c}{a}$ | C. | ±$\frac{c}{a}$ | D. | -$\frac{a}{c}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | |PP1|=|AA1|+|BB1| | B. | |PP1|=$\frac{1}{2}$|AB| | C. | |PP1|>$\frac{1}{2}$|AB| | D. | |PP1|$<\frac{1}{2}$|AB| |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
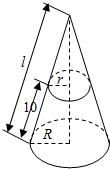 把一个圆锥截成圆台,已知圆台的上、下底面半径的比是1:2,母线长10cm.圆台侧面展开是一个$\frac{1}{4}$圆环,求:
把一个圆锥截成圆台,已知圆台的上、下底面半径的比是1:2,母线长10cm.圆台侧面展开是一个$\frac{1}{4}$圆环,求:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com