
| A. | cosα | B. | sinα | C. | 1 | D. | $\frac{1}{2}$ |
分析 先考虑分母化简,利用降次公式,正切的两角和与差公式打开,整理,可得答案.
解答 解:先考虑分母:$4{sin^2}(\frac{π}{4}+α)tan(\frac{π}{4}-α)=4\frac{{1-cos(\frac{π}{2}+2α)}}{2}•\frac{1-tanα}{1+tanα}$
=$2(1+sin2α)•\frac{cosα-sinα}{cosα+sinα}=2({cos^2}α-{sin^2}α)=2cos2α$,
故得$\frac{cos2α}{{4{{sin}^2}(\frac{π}{4}+α)tan(\frac{π}{4}-α)}}$=$\frac{cos2α}{2cos2α}=\frac{1}{2}$
故选D
点评 本题主要考察了同角三角函数关系式和万能公式的应用,两角和与差公式.属于基础题.


科目:高中数学 来源: 题型:选择题
| A. | 分层抽样 | B. | 抽签法 | C. | 随机数表法 | D. | 系统抽样法 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\frac{{3\sqrt{3}}}{2}$ | D. | $\sqrt{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(-2)>f(0)>f(1) | B. | f(-2)>f(1)>f(0) | C. | f(1)>f(0)>f(-2) | D. | f(1)>f(-2)>f(0) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
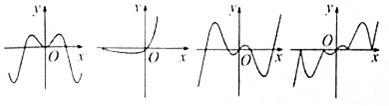
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[-\frac{1}{2},\frac{1}{2}]$ | B. | $[-\sqrt{2},\sqrt{2}]$ | C. | $(-∞,-\sqrt{2})∪(\sqrt{2},+∞)$ | D. | [-1,1] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com